Công cụ phân tích dữ liệu là một trong những tính năng tốt nhất của Excel khi chúng ta cần thực hiện phân tích thống kê nâng cao. Nếu bạn đang tìm kiếm một số thủ thuật đặc biệt để sử dụng công cụ phân tích dữ liệu trong Excel, bạn đã đến đúng nơi. Có nhiều cách để sử dụng công cụ phân tích dữ liệu trong Excel. Bài viết này sẽ thảo luận về 13 ví dụ phù hợp về việc sử dụng công cụ phân tích dữ liệu Excel. Hãy làm theo hướng dẫn đầy đủ để tìm hiểu tất cả những điều này.
Các bước để bật công cụ phân tích dữ liệu trong Excel
Trước khi phân tích tất cả các tính năng của hộp công cụ phân tích dữ liệu Excel, chúng ta phải trình bày cách cài đặt hộp công cụ này. Sau đây, chúng tôi sẽ trình bày cách bật Công cụ phân tích dữ liệu trong Excel. Để làm điều này, bạn phải thực hiện theo quy trình sau.
📌 Các bước:
- Trước tiên, hãy chuyển đến Tùy chọn từ Tệp .
- Sau đó, chuyển đến Phần bổ trợ .
- Tại đây, chọn Phần bổ trợ Excel trong Quản lý menu thả xuống.
- Và nhấp vào Bắt đầu .
- Sau đó, một cửa sổ mới sẽ xuất hiện.
- Đây, đánh dấu tùy chọn Analysis ToolPak. Và nhấp vào OK . Đây là cách bạn có thể kích hoạt hộp công cụ phân tích dữ liệu Excel.
- Bây giờ, hãy chuyển đến Phân tích trong trình đơn Dữ liệu chuyển hướng. Tại đây, bạn sẽ tìm thấy Phân tích dữ liệu tùy chọn.
13 Tính năng tuyệt vời của Công cụ phân tích dữ liệu mà bạn có thể sử dụng trong Excel
Chúng tôi sẽ sử dụng mười ba cách hiệu quả và phức tạp để sử dụng công cụ phân tích dữ liệu trong Excel. Ở đây, chúng tôi sẽ trình bày mười ba tính năng của công cụ phân tích dữ liệu Excel. Phần này cung cấp thông tin chi tiết về mười ba cách. Bạn có thể sử dụng một trong hai cho mục đích của mình, chúng có nhiều tính linh hoạt khi tùy chỉnh. Bạn nên học và áp dụng tất cả những điều này, vì chúng cải thiện khả năng tư duy và kiến thức Excel của bạn. Chúng tôi sử dụng Microsoft Office 365 phiên bản ở đây, nhưng bạn có thể sử dụng bất kỳ phiên bản nào khác tùy theo sở thích của mình.
1. Phân tích Anova
Anova cung cấp cơ hội đầu tiên để xác định yếu tố nào có ảnh hưởng đáng kể đến một tập dữ liệu nhất định. Sau khi phân tích xong, nhà phân tích thực hiện phân tích thêm về các yếu tố phương pháp luận điều đó ảnh hưởng đáng kể đến bản chất không nhất quán của các tập dữ liệu. Và anh ấy sử dụng kết quả phân tích Anova trong f-test để tạo thêm dữ liệu có liên quan đến phân tích hồi quy ước tính . Phân tích ANOVA so sánh nhiều tập dữ liệu đồng thời để xem liệu có mối liên hệ giữa chúng hay không. ANOVA là một phương pháp thống kê được sử dụng để phân tích phương sai được quan sát trong một tập dữ liệu bằng cách chia nó thành hai phần:1) Yếu tố hệ thống và 2) Yếu tố ngẫu nhiên
Công thức của Anova:
F =MSE / MST
Tại đây:
F =Hệ số Anova
MST =Tổng bình phương trung bình do xử lý
MSE =Tổng bình phương trung bình do lỗi
Anova có hai loại:một yếu tố và hai yếu tố. Phương pháp này có liên quan đến phân tích phương sai.
- Trong hai nhân tố, có nhiều biến phụ thuộc và trong một nhân tố, sẽ có một biến phụ thuộc.
- Anova đơn nhân tố tính toán ảnh hưởng của một nhân tố đơn lẻ lên một biến duy nhất. Và nó kiểm tra xem tất cả các tập dữ liệu mẫu có giống nhau hay không.
- Anova đơn nhân tố xác định sự khác biệt có ý nghĩa thống kê giữa giá trị trung bình của nhiều biến.
1.1 Phân tích Anova một yếu tố
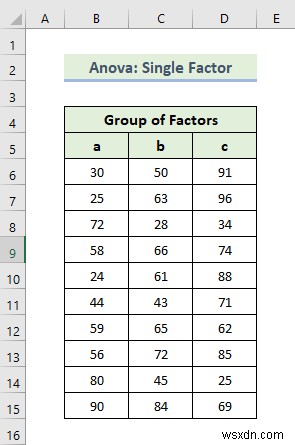
Ở đây, chúng tôi sẽ trình bày cách thực hiện phân tích Anova một nhân tố. Trước tiên, hãy để chúng tôi giới thiệu với bạn về tập dữ liệu Excel của chúng tôi để bạn có thể hiểu những gì chúng tôi đang cố gắng đạt được với bài viết này. Chúng tôi có một tập dữ liệu hiển thị nhóm các yếu tố. Hãy cùng tìm hiểu các bước để thực hiện phân tích Anova một nhân tố.
📌 Các bước:
- Trước tiên, hãy chuyển đến Dữ liệu trong dải băng trên cùng.
- Sau đó, chọn Phân tích dữ liệu công cụ.
- Khi Phân tích dữ liệu cửa sổ xuất hiện, chọn Anova:Single Factor tùy chọn.
- Sau đó, nhấp vào OK .
- Bây giờ, Anova:Single Factor cửa sổ sẽ mở ra.
- Cung cấp dữ liệu trong Phạm vi đầu vào mà bạn muốn xác định phân tích Anova bằng cách kéo qua cột hoặc hàng.
- Kiểm tra hộp có tên Nhãn ở Hàng đầu tiên .
- Trong Phạm vi đầu ra , cung cấp phạm vi dữ liệu mà bạn muốn dữ liệu được tính toán của mình lưu trữ bằng cách kéo qua cột hoặc hàng. Hoặc bạn có thể hiển thị kết quả đầu ra trong trang tính mới bằng cách chọn New Worksheet Ply và bạn cũng có thể xem kết quả đầu ra trong sổ làm việc mới bằng cách chọn Sổ làm việc mới .
- Tiếp theo, bạn phải chọn Nhãn ở hàng đầu tiên nếu bạn chọn dải dữ liệu đầu vào có nhãn.
- Sau đó, nhấp vào OK .
- Do đó, kết quả Anova sẽ như hình dưới đây.
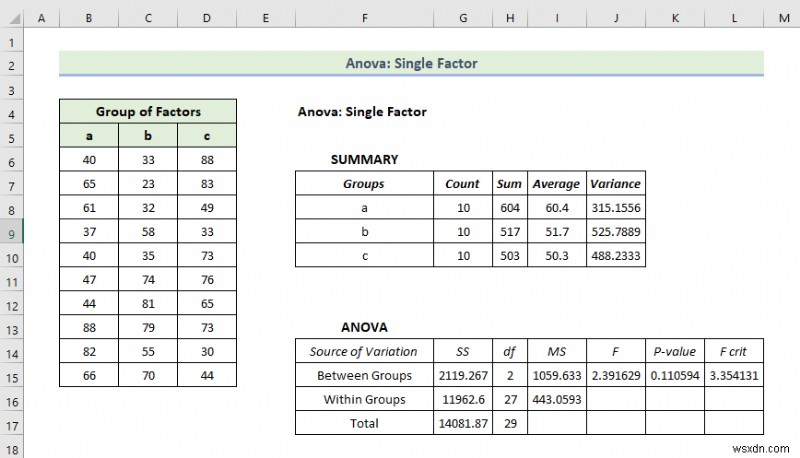
Giải thích kết quả:
- Trong bảng Tóm tắt, bạn sẽ tìm thấy giá trị trung bình và phương sai của từng nhóm. Tại đây, bạn có thể thấy mức trung bình cấp độ là 60,4 cho Nhóm a nhưng phương sai là 315.15 rất thấp so với các nhóm khác. Điều đó có nghĩa là các thành viên trong nhóm ít có giá trị hơn.
- Ở đây, kết quả Anova không quá quan trọng vì bạn chỉ đang tính toán các phương sai.
- Ở đây, giá trị P diễn giải mối quan hệ giữa các cột và các giá trị lớn hơn 0,05 nên điều này không có ý nghĩa thống kê. Và cũng không nên có mối quan hệ giữa các cột.
1.2 Anova:Hai yếu tố với sự tái tạo
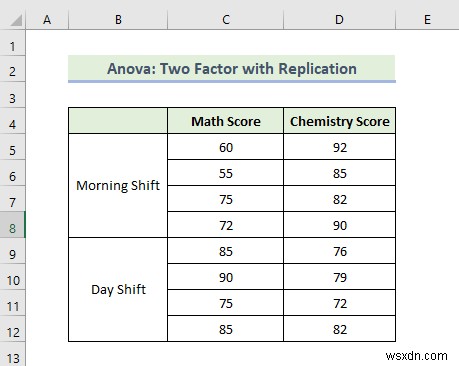
Ở đây, chúng tôi sẽ chứng minh hai yếu tố với phân tích Anova nhân rộng. Giả sử bạn có một số dữ liệu về các điểm thi khác nhau của một trường. Có hai ca trong trường đó. Một dành cho ca sáng, ca khác dành cho ca ngày. Bạn muốn thực hiện Phân tích dữ liệu của dữ liệu đã sẵn sàng để tìm mối liên hệ giữa điểm của hai ca làm việc của học sinh. Hãy cùng tìm hiểu các bước để thực hiện Anova hai yếu tố với phân tích sao chép.
📌 Các bước:
- Trước tiên, hãy chuyển đến Dữ liệu trong dải băng trên cùng.
- Sau đó, chọn Phân tích dữ liệu công cụ.
- Khi Phân tích dữ liệu cửa sổ xuất hiện, chọn Anova:Two-Factor With Replication tùy chọn.
- Sau đó, nhấp vào OK .
- Bây giờ, một cửa sổ mới sẽ xuất hiện.
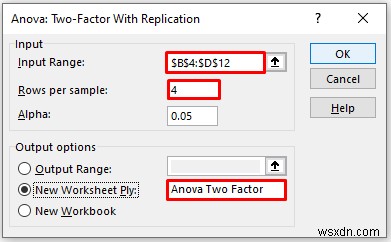
- Cung cấp dữ liệu trong Phạm vi đầu vào mà bạn muốn xác định phân tích Anova bằng cách kéo qua cột hoặc hàng.
- Tiếp theo, nhập 4 trong Hàng trên mỗi mẫu hộp như bạn có 4 hàng mỗi ca.
- Trong Phạm vi đầu ra , cung cấp phạm vi dữ liệu mà bạn muốn dữ liệu được tính toán của mình lưu trữ bằng cách kéo qua cột hoặc hàng. Hoặc bạn có thể hiển thị kết quả đầu ra trong trang tính mới bằng cách chọn New Worksheet Ply và bạn cũng có thể xem kết quả đầu ra trong sổ làm việc mới bằng cách chọn Sổ làm việc mới .
- Sau đó, nhấp vào OK .
- Kết quả là bạn sẽ thấy một trang tính mới được tạo.
- Và, hai chiều Anova kết quả được hiển thị trong trang tính này.
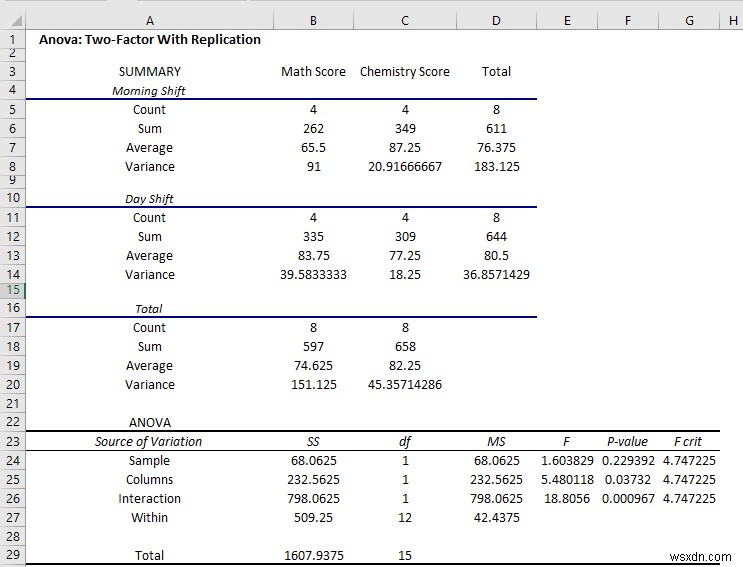
Giải thích kết quả:
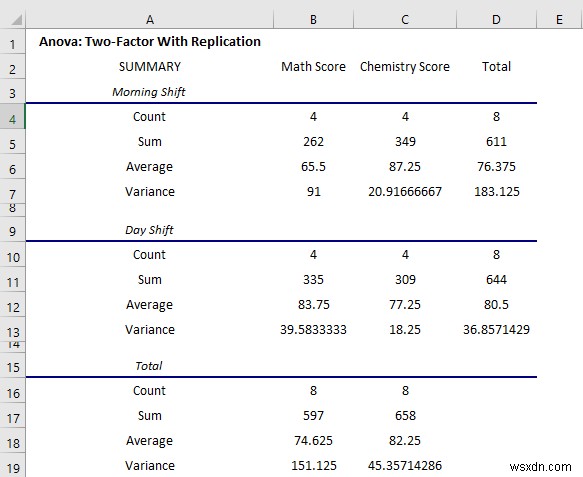
Ở đây, các bảng đầu tiên, có hiển thị tóm tắt các ca làm việc. Tóm lại:
- Điểm trung bình vào Buổi sáng thay đổi trong điểm Toán là 65,5 nhưng trong Ngày ca là 83,75
- Nhưng khi trong bài kiểm tra Hóa học, điểm trung bình của Buổi sáng ca là 87,25, nhưng trong Ngày ca là 77,25 .
- Phương sai rất cao ở mức 91 vào buổi sáng thay đổi trong bài kiểm tra Toán .
- Bạn sẽ có cái nhìn tổng quan đầy đủ về dữ liệu trong phần tóm tắt.
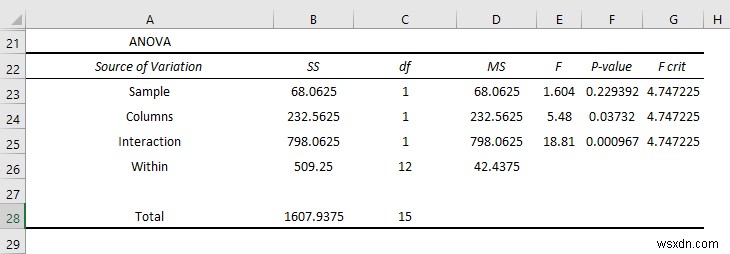
Tương tự như vậy, bạn có thể tóm tắt các tương tác và hiệu ứng riêng lẻ trong phần Anova. Tóm lại:
- Giá trị P trong số Cột là 0 . 037 có ý nghĩa về mặt thống kê, vì vậy bạn có thể nói rằng có ảnh hưởng của sự thay đổi đối với kết quả hoạt động của học sinh trong kỳ thi. Nhưng giá trị gần với giá trị alpha là 0,05 nên ảnh hưởng ít đáng kể hơn .
- Nhưng Giá trị P của các lần tương tác là 0,000967 nhỏ hơn nhiều so với giá trị alpha, vì vậy nó rất có ý nghĩa thống kê và bạn có thể nói rằng ảnh hưởng của sự thay đổi đối với cả hai kỳ thi là rất cao.
1.3 Anova:Hai yếu tố không cần sao chép
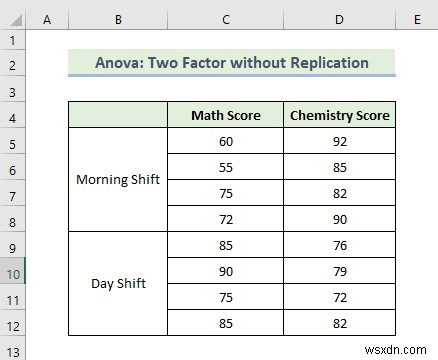
Bây giờ, chúng ta sẽ thực hiện phân tích phương sai bằng cách làm theo phương pháp của hai yếu tố mà không cần phân tích Anova lặp lại. Chúng tôi Giả sử bạn có một số dữ liệu về các điểm thi khác nhau của một trường. Có hai ca ở trường đó. Một dành cho ca sáng, ca khác dành cho ca ngày. Bạn muốn thực hiện Phân tích dữ liệu của dữ liệu đã sẵn sàng để tìm mối liên hệ giữa điểm của hai ca làm việc của học sinh. Hãy cùng tìm hiểu các bước để chấm hai yếu tố ANOVA mà không cần phân tích sao chép.
📌 Các bước:
- Trước tiên, hãy chuyển đến Dữ liệu trong dải băng trên cùng.
- Sau đó, chọn Phân tích dữ liệu công cụ.
- Khi Phân tích dữ liệu cửa sổ xuất hiện, chọn “ Anova:Two-Factor Without Replication ”Tùy chọn.
- Sau đó, nhấp vào OK .
- Bây giờ, một cửa sổ mới sẽ xuất hiện.
- Cung cấp dữ liệu trong Phạm vi đầu vào mà bạn muốn xác định phân tích Anova bằng cách kéo qua cột hoặc hàng.
- Trong Phạm vi đầu ra , cung cấp phạm vi dữ liệu mà bạn muốn dữ liệu được tính toán của mình lưu trữ bằng cách kéo qua cột hoặc hàng. Hoặc bạn có thể hiển thị kết quả đầu ra trong trang tính mới bằng cách chọn New Worksheet Ply và bạn cũng có thể xem kết quả đầu ra trong sổ làm việc mới bằng cách chọn Sổ làm việc mới .
- Tiếp theo, bạn phải kiểm tra Nhãn nếu phạm vi dữ liệu đầu vào có nhãn.
- Sau đó, nhấp vào OK .
- Kết quả là bạn sẽ thấy một trang tính mới được tạo.
- Do đó, bạn sẽ nhận được kết quả Anova hai chiều như hình dưới đây.
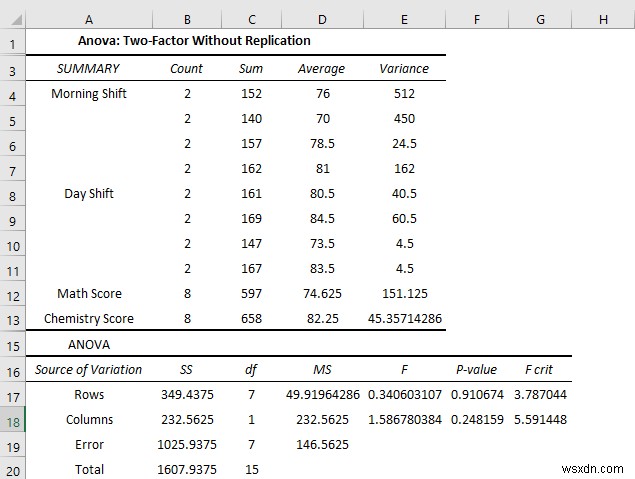
Giải thích kết quả:
- Điểm trung bình vào Buổi sáng thay đổi trong điểm Toán là 65 . 5 nhưng trong Ngày ca là 83,75
- Nhưng khi trong bài kiểm tra Hóa học, điểm trung bình của Buổi sáng ca là 87 nhưng trong Ngày ca là 77,25.
- Giá trị P trong số Cột là 0,24 có ý nghĩa về mặt thống kê, vì vậy bạn có thể nói rằng có ảnh hưởng của sự thay đổi đối với kết quả hoạt động của học sinh trong kỳ thi. Nhưng giá trị gần với giá trị alpha là 0,05 nên ảnh hưởng ít đáng kể hơn .
Đọc thêm: Cách thêm phân tích dữ liệu trong Excel (với 2 bước nhanh)
2. Phân tích tương quan
Bây giờ, chúng ta sẽ thực hiện phân tích dữ liệu tương quan, đây là một tính năng tuyệt vời của hộp công cụ phân tích dữ liệu Excel. Trong thống kê, hệ số tương quan hay hệ số tương quan là tham số thể hiện sự gắn kết giữa hai biến số với đại lượng dao động liên tục của một biến số khác. Giá trị của nó nằm trong khoảng từ -1 đến +1 . Do đó, nó có ba trạng thái xác định quan hệ biến số. Đó là:
- -1 biểu thị mối tương quan nghịch, có nghĩa là các biến thay đổi theo hướng ngược lại.
- +1 cho biết mối tương quan thuận có nghĩa là các biến thay đổi theo cùng một hướng.
- 0 cho biết không có mối tương quan, nghĩa là không có chuyển động rõ ràng theo bất kỳ hướng nào của một biến khi thay đổi giá trị của các biến khác.
Ở đây, chúng tôi có một tập dữ liệu chứa hai giá cổ phiếu trong các khoảng thời gian khác nhau. Hãy cùng tìm hiểu các bước để thực hiện phân tích dữ liệu tương quan.
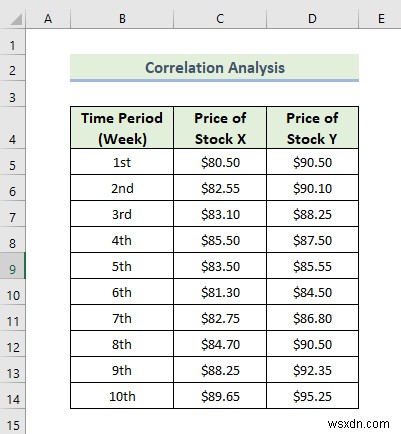
📌 Các bước:
- Trước tiên, hãy chuyển đến Dữ liệu trong dải băng trên cùng.
- Sau đó, chọn Phân tích dữ liệu công cụ.
- Khi Phân tích dữ liệu cửa sổ xuất hiện, chọn Tương quan tùy chọn.
- Tiếp theo, nhấp vào OK .
- Bây giờ, một cửa sổ mới sẽ xuất hiện.
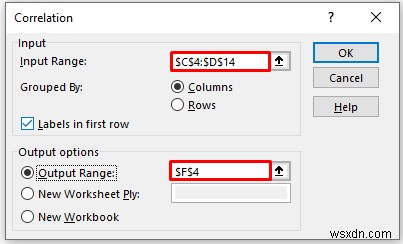
- Cung cấp dữ liệu trong Phạm vi đầu vào mà bạn muốn tính toán mối tương quan bằng cách kéo qua cột hoặc hàng.
- Bây giờ, bạn phải kiểm tra Cột trong tùy chọn Được nhóm theo tùy chọn.
- Trong Phạm vi đầu ra , cung cấp phạm vi dữ liệu mà bạn muốn dữ liệu được tính toán của mình lưu trữ bằng cách kéo qua cột hoặc hàng. Hoặc bạn có thể hiển thị kết quả đầu ra trong trang tính mới bằng cách chọn New Worksheet Ply và bạn cũng có thể xem kết quả đầu ra trong sổ làm việc mới bằng cách chọn Sổ làm việc mới .
- Tiếp theo, bạn phải chọn Nhãn ở hàng đầu tiên nếu phạm vi dữ liệu đầu vào có nhãn.
- Sau đó, nhấp vào OK .
- Do đó, bạn sẽ nhận được kết quả tương quan sau đây.
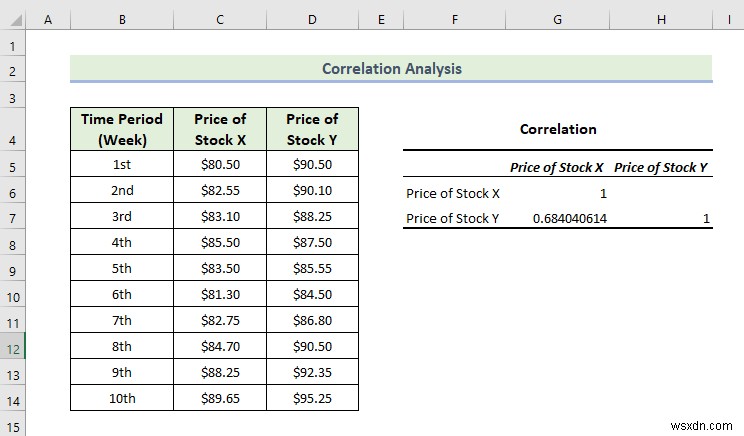
Từ tính toán trên, chúng ta có thể thấy mối tương quan thuận có nghĩa là các biến thay đổi theo cùng một hướng.
Đọc thêm: Cách phân tích dữ liệu chuỗi thời gian trong Excel (Với các bước dễ dàng)
3. Phân tích hiệp phương sai
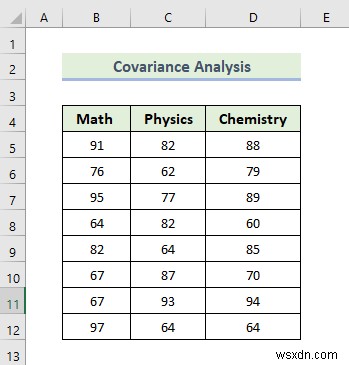
Bây giờ, chúng ta sẽ thực hiện phân tích dữ liệu hiệp phương sai, đây là một tính năng tuyệt vời của công cụ phân tích dữ liệu Excel. Hiệp phương sai của hai biến là thước đo cách một trong số chúng ảnh hưởng đến biến kia. Rõ ràng, đó là một đánh giá cần thiết về độ lệch giữa hai biến. Hơn nữa, các biến không cần phải phụ thuộc vào nhau. Hãy cùng tìm hiểu các bước để thực hiện phân tích dữ liệu hiệp phương sai.
📌 Các bước:
- Trước tiên, hãy chuyển đến Dữ liệu trong dải băng trên cùng.
- Sau đó, chọn Phân tích dữ liệu công cụ.
- Khi Phân tích dữ liệu cửa sổ xuất hiện, chọn Hiệp phương sai tùy chọn.
- Sau đó, nhấn Enter .
- Sau đó, nhấp vào OK .
- Bây giờ, một cửa sổ mới sẽ xuất hiện.
- Cung cấp dữ liệu trong Phạm vi đầu vào mà bạn muốn tính hiệp phương sai bằng cách kéo qua cột hoặc hàng.
- Bây giờ, bạn phải kiểm tra Cột trong tùy chọn Được nhóm theo phần.
- Trong Phạm vi đầu ra , cung cấp phạm vi dữ liệu mà bạn muốn dữ liệu được tính toán của mình lưu trữ bằng cách kéo qua cột hoặc hàng. Hoặc bạn có thể hiển thị kết quả đầu ra trong trang tính mới bằng cách chọn New Worksheet Ply và bạn cũng có thể xem kết quả đầu ra trong sổ làm việc mới bằng cách chọn Sổ làm việc mới .
- Tiếp theo, bạn phải chọn Nhãn ở hàng đầu tiên nếu phạm vi dữ liệu đầu vào có nhãn.
- Sau đó, nhấp vào OK .
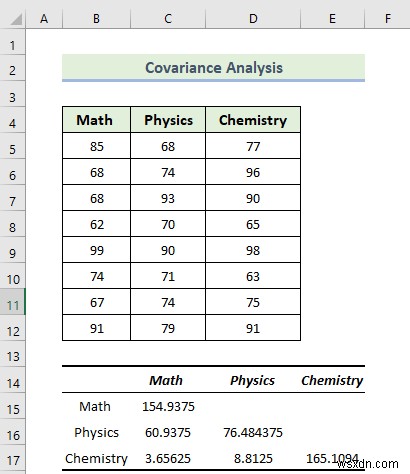
- Do đó, bạn sẽ nhận được kết quả hiệp phương sai sau.
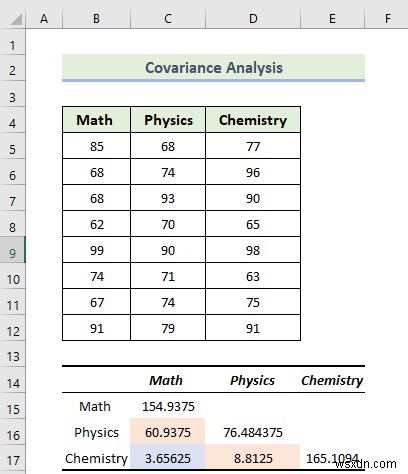
Giải thích kết quả:
Ma trận tương quan cho phép chúng ta đánh giá các mối quan hệ giữa nhiều biến và các biến đơn. Phần đánh dấu từ hình ảnh sau đây cho biết phương sai cho từng chủ đề.
- Phương sai của Math là 154,9375 và phương sai của Vật lý là 76.484375 . Tiếp theo, phương sai của Hóa học là 154,9375.
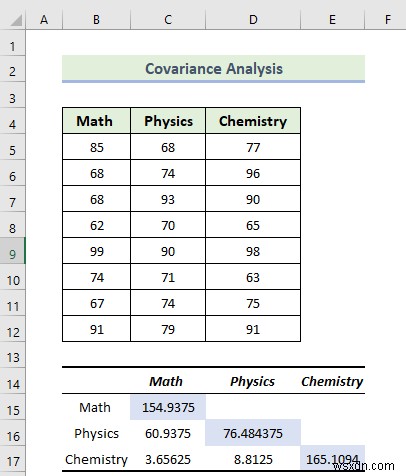
Phần đánh dấu từ hình ảnh sau đây cho biết các giá trị của phương sai giữa hai đối tượng. Toán và Vật lý, Toán và Hóa học và Vật lý và Lịch sử có giá trị phương sai lần lượt là 60,9375 , 3,65625, và 8.8125. Khi hiệp phương sai, trong trường hợp này, là dương, nó chỉ ra rằng các biến tương ứng với nhau, có nghĩa là khi một biến tăng lên, biến kia có xu hướng tăng cùng với nó.
Đọc thêm: [Đã sửa:] Phân tích dữ liệu không hiển thị trong Excel (2 giải pháp hiệu quả)
4. Phân tích thống kê mô tả
Bây giờ, chúng tôi sẽ trình bày cách thực hiện phân tích thống kê mô tả. Hộp công cụ phân tích dữ liệu Excel cho phép chúng tôi thực hiện phân tích thống kê mô tả để phân tích tập dữ liệu để xác định các đặc điểm của nó. Ở đây, chúng tôi có một tập dữ liệu chứa điểm vật lý của mỗi học sinh. Hãy cùng tìm hiểu các bước để thực hiện phân tích dữ liệu tương quan.
📌 Các bước:
- Trước tiên, hãy chuyển đến Dữ liệu trong dải băng trên cùng.
- Sau đó, chọn Phân tích dữ liệu công cụ.
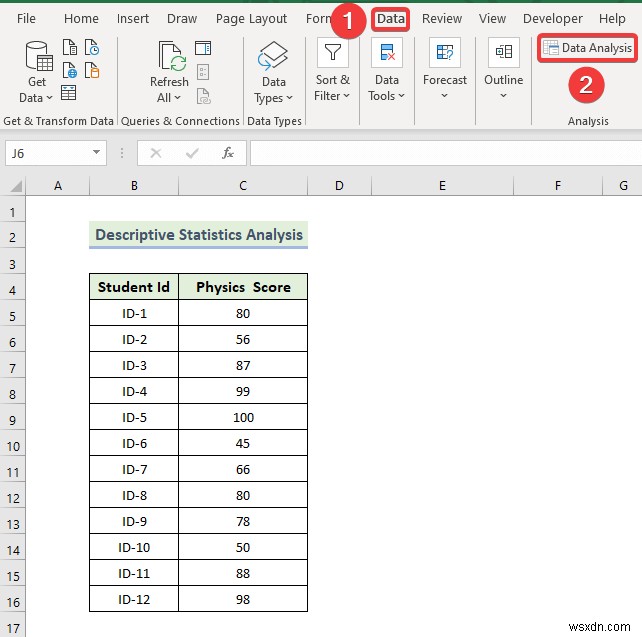
- Khi Phân tích dữ liệu cửa sổ xuất hiện, chọn Thống kê mô tả tùy chọn.
- Sau đó, nhấp vào OK .
- Bây giờ, một cửa sổ mới sẽ xuất hiện.
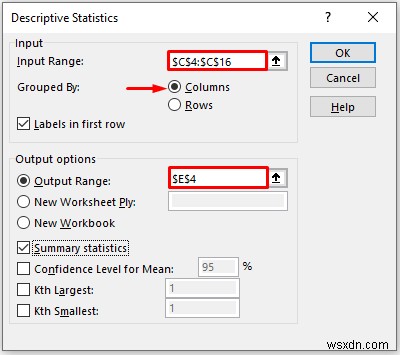
- Cung cấp dữ liệu trong Phạm vi đầu vào box, that you want to calculate the descriptive statistics by dragging through the column or row.
- Now, you have to check the Columns option in the Grouped By phần.
- In the Output Range box, provide the data range that you want your calculated data to store by dragging through the column or row. Or you can show the output in the new worksheet by selecting New Worksheet Ply and you can also see the output in the new workbook by selecting New Workbook .
- Then, check the Summary statistics .
- Then, click on OK .
- As a consequence, you will get the following covariance result.
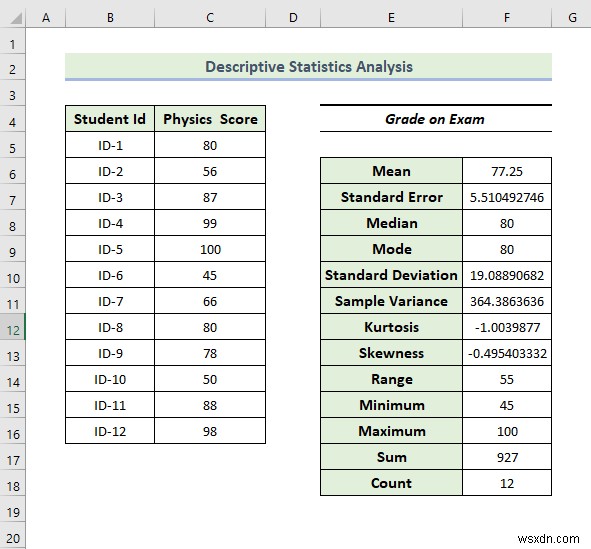
- The above result gives us the characteristics of two variables, i.e. mean, median, standard deviation, and maximum and minimum value of the dataset, which are respectively 77.25, 80, 19.088, 45, and 100.
Đọc thêm: How to Use Analyze Data in Excel (5 Easy Methods)
5. Exponential Smoothing Analysis
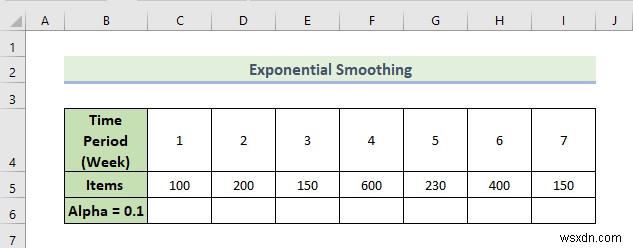
Now, we are going to demonstrate how to do an exponential smoothing analysis. The Excel data analysis toolpak allows us to do exponential smoothing in order to make appropriate decisions regarding business volume. Here, we have a dataset containing a number of items sold in different weeks by a manufacturing company. Let’s walk through the steps to do an exponential smoothing data analysis.
📌 Các bước:
- First, go to the Data tab in the top ribbon.
- Then, select the Data Analysis tool.
- When the Data Analysis window appears, select the Exponential Smoothing option.
- Then, click on OK .
- Now, a new window sẽ xuất hiện.
- Provide data in the Input Range box, that you want to calculate the exponential smoothing by dragging through the column or row.
- Now, you have to enter 0.9 in the Damping factor hộp. Here, we damping 1-alpha
- In the Output Range box, provide the data range that you want your calculated data to store by dragging through the column or row. Or you can show the output in the new worksheet by selecting New Worksheet Ply and you can also see the output in the new workbook by selecting New Workbook .
- Next, you have to check the Labels if the input data range with the label.
- Then, check the Chat Output .
- Then, click on OK .
- As a consequence, you will get the following exponential smoothing result and chart for 0.1 alpha.
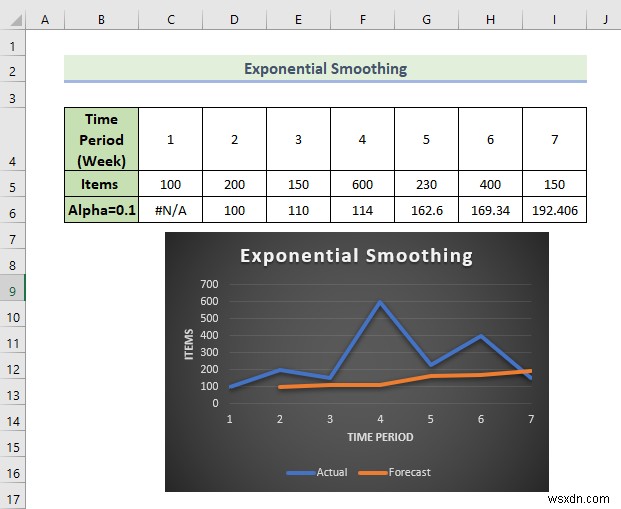
Here, from the above result, we can say that Excel can not provide data for the first value in this method. If we use a large damping factor, we will get more smooth peaks and valleys.
6. F-Test Two-Sample for Variances Analysis
Now, we are going to do an F-test for two sample variances. Using the variance of two variables, the F-test provides statistical analysis in Excel. Here, we have a dataset containing two items’ sales prices in different weeks by a manufacturing company. Let’s walk through the steps to do an f-test for two sample variances.
📌 Các bước:
- First, go to the Data tab in the top ribbon.
- Then, select the Data Analysis tool.

- When the Data Analysis window appears, select the F-Test Two-Sample for Variances tùy chọn.
- Then, click on OK .
- Now, a new window sẽ xuất hiện.
- Provide data in the Input Range box, that you want to calculate the F-test by dragging through the column or row.
- In the Output Range box, provide the data range that you want your calculated data to store by dragging through the column or row. Or you can show the output in the new worksheet by selecting New Worksheet Ply and you can also see the output in the new workbook by selecting New Workbook .
- Next, you have to check the Labels if the input data range with the label.
- Then, click on OK .
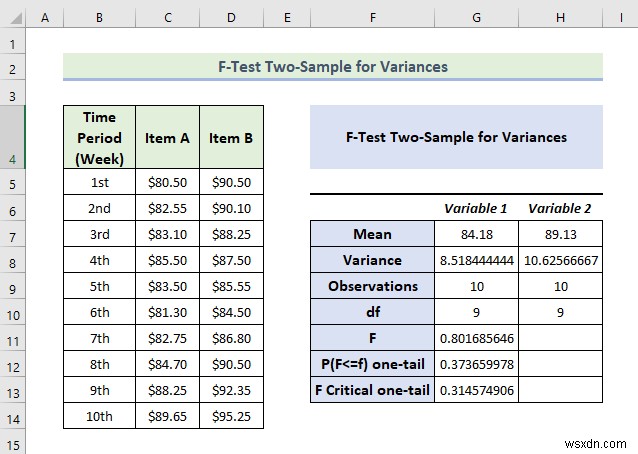
- As a consequence, you will get the following result of an F-test for two sample variances.
Explanation of the Result:
- From the above data, we can see that the mean value of variable 2 is greater than variable 1.
- We also know that if the value F is greater than F Critical one-tail value, in this case, we can say it doesn’t follow null hypothesis. In the above data, the value of F is .8016 and the value of F Critical one-tail is 0.3145 which indicates F is much greater than F critical one-tail. In other words, the variances between two variables don’t match.
7. Moving Average Analysis
Now, we are going to do a moving average analysis which is one of the best features of Excel data analysis toolpak.. The moving average means the time period of the average is the same but it keeps moving when new data is added. Am moving average smooths out any irregularities (peaks and valleys) from data to easily recognize trends. The larger the interval period is to calculate the moving average, the more fluctuations smoothing occurs. As more data points are included in each calculated average. Here, we have a dataset containing a number of items sold in different weeks by a manufacturing company. Let’s walk through the steps to do a moving average analysis.
📌 Các bước:
- First, go to the Data tab in the top ribbon.
- Then, select the Data Analysis tool.
- When the Data Analysis window appears, select the Moving Average tùy chọn.
- Then, click on OK .
In the Moving Average pop-up box,
- Provide data in the Input Range box, that you want to calculate the moving average by dragging through the column or row.
- Write the number of intervals the Interval .
- In the Output Range box, provide the data range that you want your calculated data to store by dragging through the column or row. Or you can show the output in the new worksheet by selecting New Worksheet Ply and you can also see the output in the new workbook by selecting New Workbook .
- If you want to see the trendline of your data with a chart then check the Chart Output otherwise leave it.
- Next, you have to check the Labels in the first row if the input data range with the label.
- Then, click on OK .
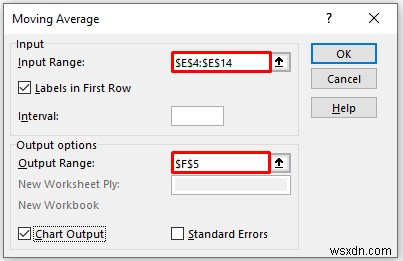
- As a consequence, you will get the moving average of the data along with an Excel trendline showing both the original data and the moving average value with smoothed fluctuations.
Bài đọc tương tự
- How to Analyze Quantitative Data in Excel (with Easy Steps)
- Analyze Large Data Sets in Excel (6 Effective Methods)
- Cách Phân tích Dữ liệu Quy mô Likert trong Excel (với các Bước Nhanh)
- Phân tích Dữ liệu Định tính từ Bảng câu hỏi trong Excel
8. Random Number Generation
Now, we are going to generate a random number. The Excel data analysis toolpak allows us to generate random numbers with different criteria. Let’s walk through the steps to do a moving average analysis.
📌 Các bước:
- First, go to the Data tab in the top ribbon.
- Then, select the Data Analysis tool.
- When the Data Analysis window appears, select the Descriptive Statistics tùy chọn.
- Then, click on OK .
In the Random Number Generation pop-up box,
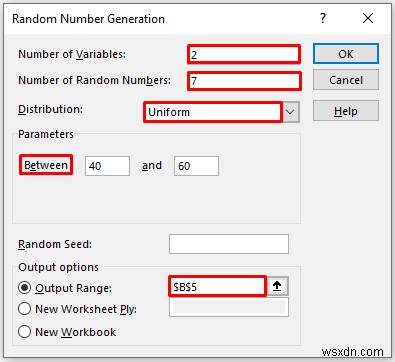
- Provide data on the Number of Variables which indicates the number of columns of random numbers that you want in your worksheet. Here, we enter 2 as we want 2 columns.
- Next, you have to provide data in the Number of Random Numbers which refers to the number of rows that you want in your worksheet. Here, enter 7 which means we want 7 rows in our worksheet.
- Then, select the uniform in the Distribution Here, Distribution means which kinds of distribution of random numbers you want.
- Here, parameters indicate the boundaries of your distribution. In this example, we 40 to 60.
- In the Output Range box, provide the data range that you want your calculated data to store by dragging through the column or row. Or you can show the output in the new worksheet by selecting New Worksheet Ply and you can also see the output in the new workbook by selecting New Workbook .
- Then, click on OK .
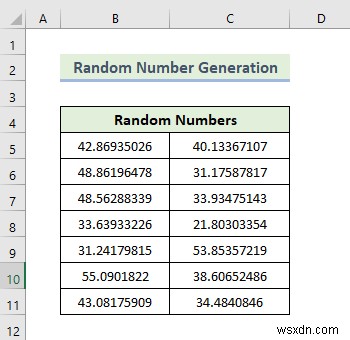
- As a consequence, you will be able to generate random numbers with some specified criteria as shown below.
9. Rank and Percentile Analysis
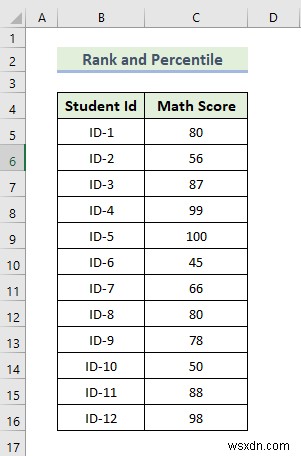
Now, we are going to do rank and percentile analysis. Here, we have a dataset containing students’ ID and their Math exam scores. We are going to calculate the rank and percentile of each student’s math exam score. Let’s walk through the steps to do rank and percentile analysis.
📌 Các bước:
- First, go to the Data tab in the top ribbon.
- Then, select the Data Analysis tool.
- When the Data Analysis window appears, select the Rank and Percentile tùy chọn.
- Then, click on OK .
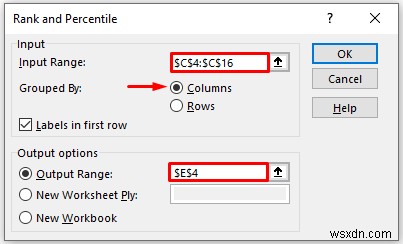
In the Rank and Percentile pop-up box,
- Provide data in the Input Range box, that you want to calculate the moving average by dragging through the column or row.
- Now, you have to check the Columns option in the Grouped By phần.
- In the Output Range box, provide the data range that you want your calculated data to store by dragging through the column or row. Or you can show the output in the new worksheet by selecting New Worksheet Ply and you can also see the output in the new workbook by selecting New Workbook .
- Next, you have to check the Labels in the first row if the input data range with the label.
- Then, click on OK .
- As a consequence, you will get the rank and percentile for each student’s exam score as shown below.
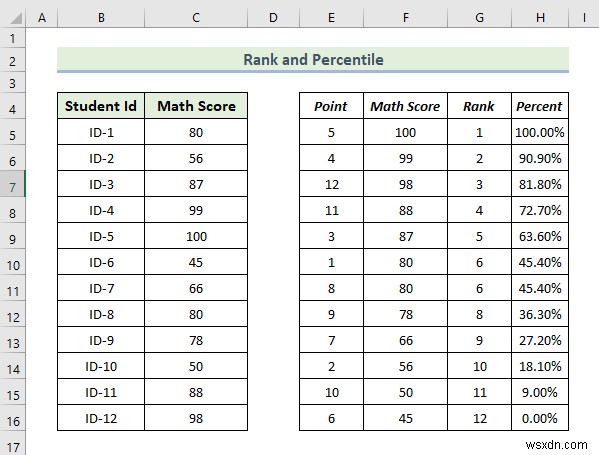
From the above result, we can see that we are able to calculate the rank and percentile of each student’s mark. Here, the Rank 1 mark is 100 which is ID-5’s math score, and the last rank mark is 45 which is ID-6’s math score.
10. Regression Analysis
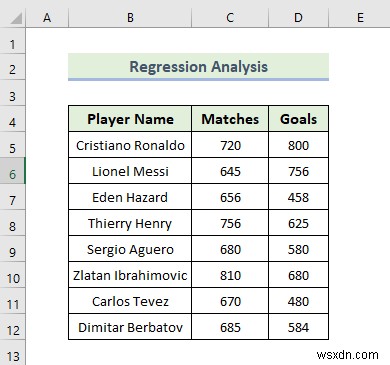
Now, we are going to do regression analysis. Regression analysis is a part of statistics that helps to predict values depending on two or more variables. Here, we have a dataset containing the player name, the number of matches played by each player, and the number of goals given by each player. Let’s walk through the steps to do regression analysis.
📌 Các bước:
- First, go to the Data tab in the top ribbon.
- Then, select the Data Analysis tool.
- When the Data Analysis window appears, select the Regression tùy chọn.
- Then, click on OK .
In the Regression pop-up box,
- Provide data in the Input Range box, and provide the data ranges in the Input X Range and Input Y Range boxes.
- In the Output Range box, provide the data range that you want your calculated data to store by dragging through the column or row. Or you can show the output in the new worksheet by selecting New Worksheet Ply and you can also see the output in the new workbook by selecting New Workbook .
- Next, you have to check the Labels if the input data range with the label.
- You also have to check the Residuals option to get the output value.
- Then, click on OK .
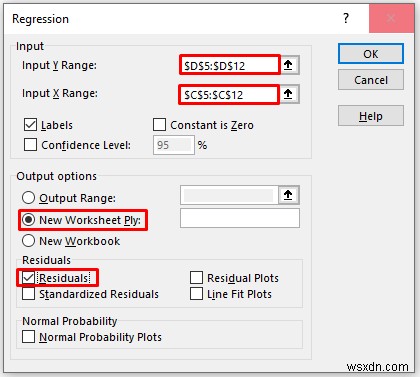
- As a consequence, you will get the following result of the regression analysis.
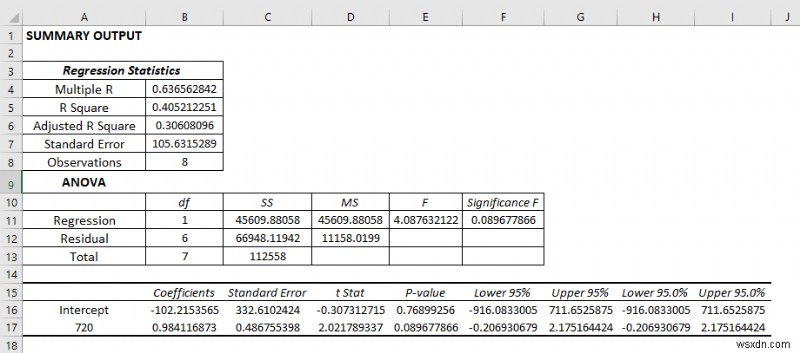
Explanation of the Regression Analysis Result:
Regression Statistics:
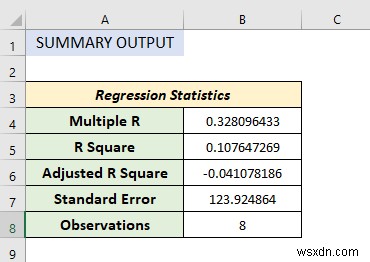
Regression statistics is an array of various parameters that describe how well the measured linear regression is.
- Multiple R is a correlation coefficient parameter that indicates the correlation between variables. Its value ranges from -1 to +1. The bigger the value, the stronger the correlative relationships are.
- R Square symbolizes the coefficient of determination. It indicates the scale by how well the data model fits the regression analysis.
- The adjusted R square is used in multiple variables in regression analysis.
- Standard Error is another parameter that shows a healthy fit of any regression analysis. The smaller the standard error the more accurate the linear regression equation. It shows the average distance of data points from the linear equation.
Anova:
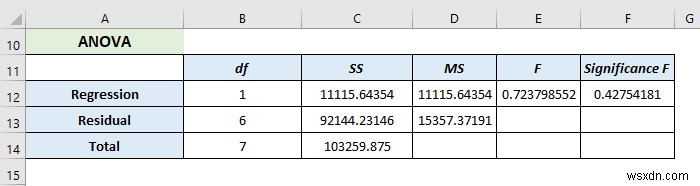
It analyses the variance of the data model.
- Here, df represents the degree of freedom.
- SS( sum of squares) symbolizes the good-to-fit parameter.
- MS means the Mean Square.
- F refers to the Null Hypothesis. It tests the overall significance of the regression model
- Significance of F means the P-value of F.
Co-efficient Outcome:

It helps to determine Y values easily.
Residual Output:
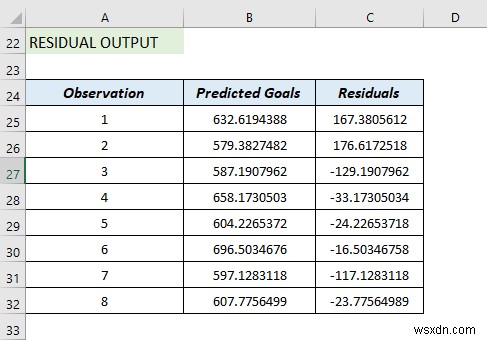
So, it compares the estimated value with the calculated value.
11. t-Test Analysis
Now, we are going to do a T-Test analysis of the dataset. The T-Test is of three types:
- Paired two samples for means
- Two samples assuming equal variances
- Two- samples using unequal variances
This section provides extensive details on the three types of t-Test analysis. You can use either one for your purpose, they have a wide range of flexibility when it comes to customization.
11.1 t-Test:Paired Two Sample for Means
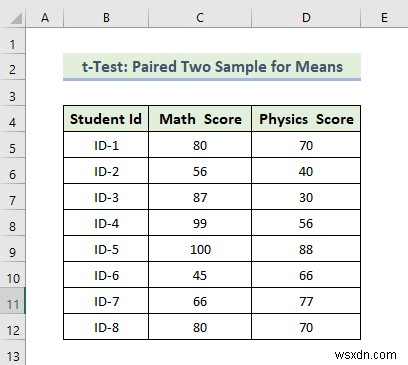
Now, we are going to do a t-Test:Paired Two Sample for Means. Here, we have a dataset containing the Students’ IDs and each student’s Math and Physics scores. Let’s walk through the steps to do a t-Test:Paired Two Sample for Means analysis.
📌 Các bước:
- First, go to the Data tab in the top ribbon.
- Then, select the Data Analysis tool.
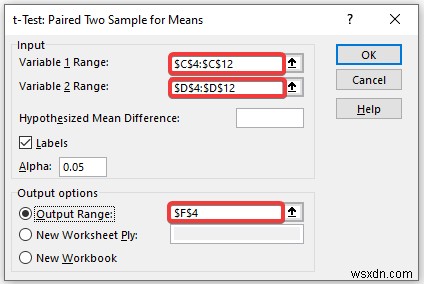
- When the Data Analysis window appears, select the t-Test:Paired Two Samples for Means tùy chọn.
- Then, click on OK .
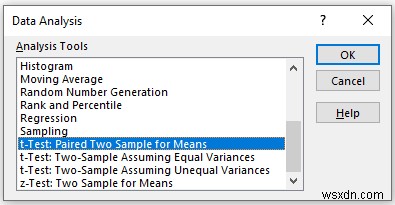
In the t-Test:Paired Two Sample for Means pop-up box,
- Provide data in the Input box, and provide the data ranges in the Variable 1 Range and Variable 2 Range boxes.
- In the Output Range box, provide the data range that you want your calculated data to store by dragging through the column or row. Or you can show the output in the new worksheet by selecting New Worksheet Ply and you can also see the output in the new workbook by selecting New Workbook .
- Next, you have to check the Labels if the input data range with the label.
- Then, click on OK .

- As a consequence, you will get the following result of the t-Test:Paired Two Sample for Means .
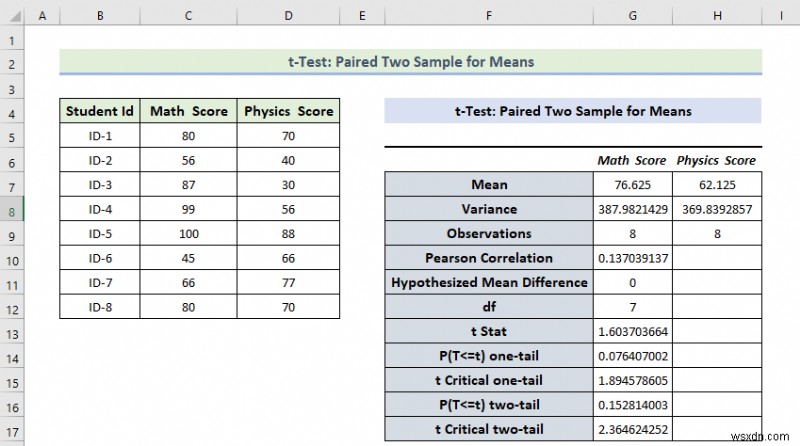
Explanation of the Result:
- Here, we can see that the Mean Value of the Math Score is greater than the mean value of the Physics Score.
- The variance of the Math Score is also greater than the variance of the Physics Score.
- If t Stat is greater than t Critical two-tail, in this condition we can’t eliminate null hypothesis. In the above calculation, we can see that t Stat is and t Critical two-tail value is respectively 1.603 and 2.36464 . That means 1.603<2.36464 , it doesn’t match the null hypothesis. In other words, the variances between two variables don’t match.
11.2 t-Test Two-Sample Assuming Equal Variances
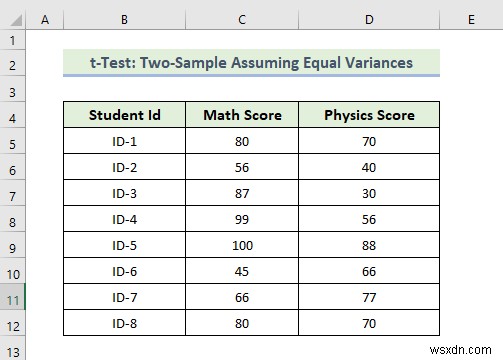
Now, we are going to do a t-Test:Two-Sample Equal Variances . Here, we have a dataset containing the Students’ IDs and each student’s Math and Physics scores. Here, equal variance means that we have taken our data from regular distribution populations. Let’s walk through the steps to do a t-Test:Two-Sample Equal Variances analysis.
📌 Các bước:
- First, go to the Data tab in the top ribbon.
- Then, select the Data Analysis tool.
- When the Data Analysis window appears, select the t-Test:Two-Sample Equal Variances tùy chọn.
- Then, click on OK .
In the t-Test:Paired Two Sample Equal Variances pop-up box,
- Provide data in the Input box, and provide the data ranges in the Variable 1 Range and Variable 2 Range boxes.
- In the Output Range box, provide the data range that you want your calculated data to store by dragging through the column or row. Or you can show the output in the new worksheet by selecting New Worksheet Ply and you can also see the output in the new workbook by selecting New Workbook .
- Next, you have to check the Labels if the input data range with the label.
- Then, click on OK .
- As a consequence, you will get the following result of the t-Test:Two-Sample Equal Variances .
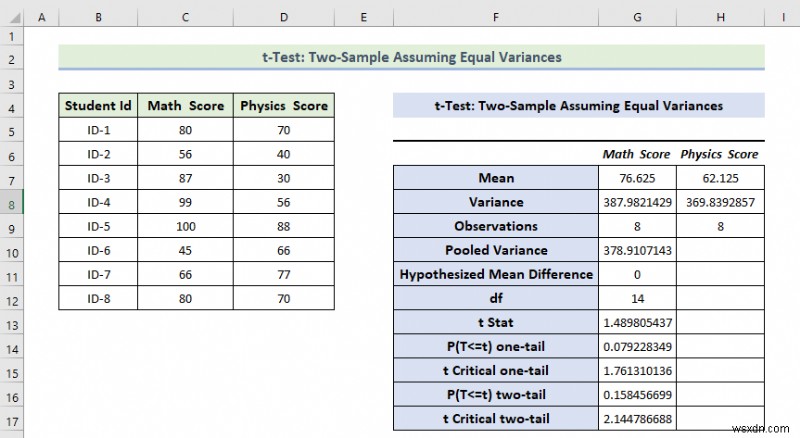
Explanation of the Result:
- Here, we can see that the Mean Value of the Math Score is greater than the mean value of the Physics Score.
- The variance of the Math Score is also greater than the variance of the Physics Score.
- If t Stat is greater than t Critical two-tail, in this condition we can’t eliminate the null hypothesis. In the above calculation, we can see that t Stat is and t Critical two-tail value is respectively 1.48 and 2.144 . That means 1.48<2.144 , it doesn’t match the null hypothesis. In other words, the variances between two variables don’t match.
11.3 t-Test:Two-Sample Assuming Unequal Variances
Now, we are going to do a t-Test:Two-Sample Unequal Variances. Here, we have a dataset containing the Students’ IDs and each student’s Math and Physics scores. Here, unequal variance means that we have taken our data from irregular distribution populations. Let’s walk through the steps to do a t-Test:Two-Sample Unequal Variances analysis.
📌 Các bước:
- First, go to the Data tab in the top ribbon.
- Then, select the Data Analysis tool.
- When the Data Analysis window appears, select the t-Test:Two-Sample Unequal Variances tùy chọn.
- Then, click on OK .
In the t-Test:Paired Two Sample Unequal Variances pop-up box,
- Provide data in the Input box, and provide the data ranges in the Variable 1 Range and Variable 2 Range boxes.
- In the Output Range box, provide the data range that you want your calculated data to store by dragging through the column or row. Or you can show the output in the new worksheet by selecting New Worksheet Ply and you can also see the output in the new workbook by selecting New Workbook .
- Next, you have to check the Labels if the input data range with the label.
- Then, click on OK .
- As a consequence, you will get the following result of the t-Test:Two-Sample Unequal Variances.
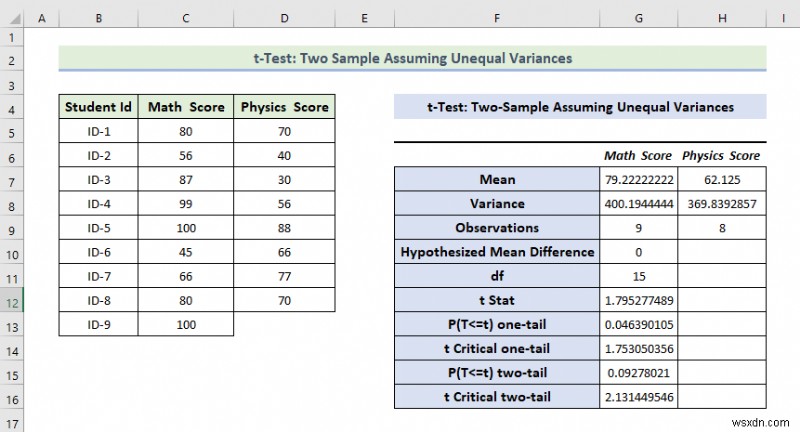
Explanation of the Result:
- Here, we can see that the Mean Value of the Math Score is greater than the mean value of the Physics Score.
- From the above result, we can see the variance of the Math Score is also greater than the variance of the Physics Score.
- If t Stat is greater than t Critical two-tail, in this condition we can’t eliminate null hypothesis. In the above calculation, we can see that t Stat is and t Critical two-tail value is respectively 79 and 2.131 . That means 1.79<2.131 , it doesn’t match the null hypothesis. In other words, the variances between two variables don’t match.
12. z-Test:Two Sample for Means
Now, we are going to do a z-Test:Two-Sample Means. Here, we have a dataset containing the Students’ IDs and each student’s Math and Physics scores. Here we will use the VAR.P function to calculate the variance of both variables of the following dataset. Let’s walk through the steps to do a z-Test:Two-Sample Means analysis.
📌 Các bước:
- First of all, to calculate the variance of the Math score, we will use the following formula in the cell D14:
=VAR.P(C5:C12)
- Sau đó, nhấn Enter .
- As a consequence, you will get the following variance of Match Score.
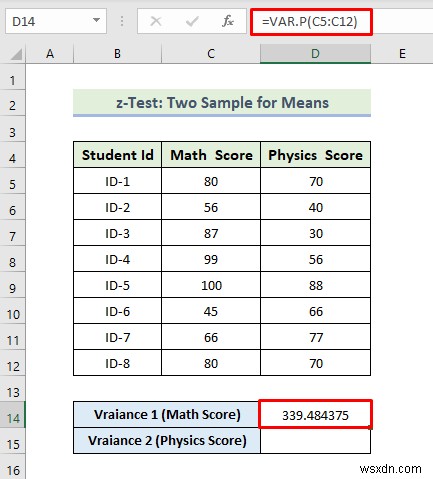
- Next, to calculate the variance of the Physics score, we will use the following formula in the cell D15:
=VAR.P(D5:D12)
- Sau đó, nhấn Enter .
- As a consequence, you will get the following variance of Physics Score.
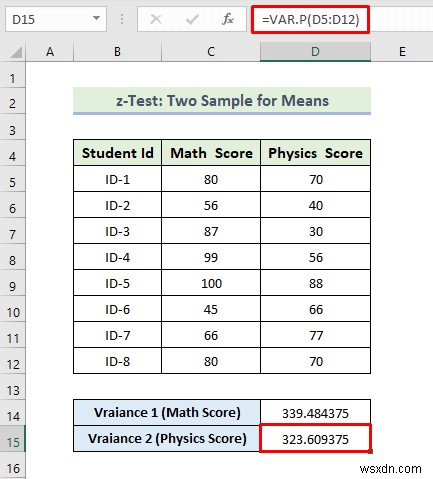
- First, go to the Data tab in the top ribbon.
- Then, select the Data Analysis tool.
- When the Data Analysis window appears, select the z-Test:Two-Sample Means tùy chọn.
- Then, click on OK .
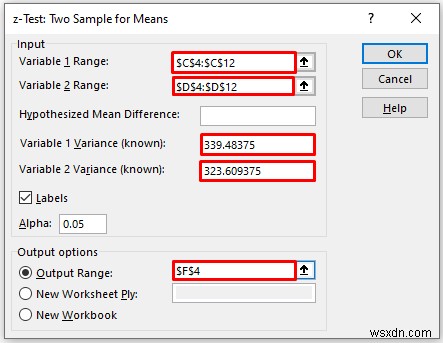
In the z-Test:Two-Sample Means pop-up box,
- Provide data in the Input box, and provide the data ranges in the Variable 1 Range and Variable 2 Range boxes.
- In the Output Range box, provide the data range that you want your calculated data to store by dragging through the column or row. Or you can show the output in the new worksheet by selecting New Worksheet Ply and you can also see the output in the new workbook by selecting New Workbook .
- You have to enter the value variance of Math and Physics Score respectively in the Variable 1 Variance (known) and Variable 2 Variance (known)
- Next, you have to check the Labels if the input data range with the label.
- Then, click on OK .
- As a consequence, you will get the following result of the z-Test:Two-Sample Means tùy chọn.
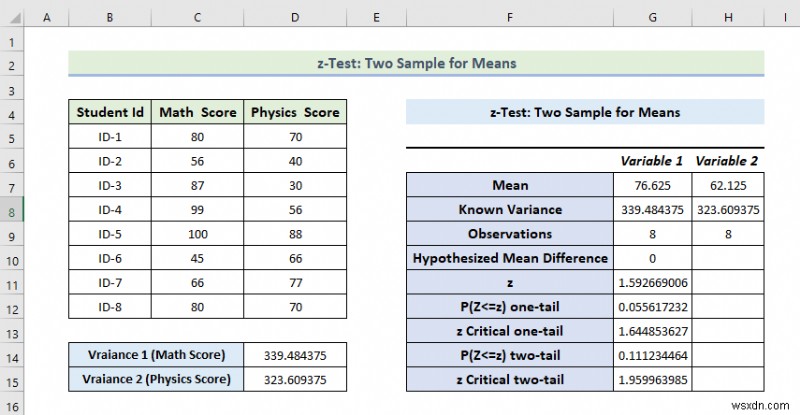
Explanation of the Result:
- Here, we can see that the Mean Value of the Math Score is greater than the mean value of the Physics Score.
- From the above result, we can see the variance of the Math Score is also greater than the variance of the Physics Score.
- If Z is less than Z critical two-tall, in this condition we can’t eliminate null hypothesis. In the above calculation, we can see that z and z Critical two-tail value is respectively 52 and 1.95 . That means 1.52 <1.95 , which matches the null hypothesis. In other words, the variances between two variables match.
Đọc thêm: How to Perform Case Study Using Excel Data Analysis
13. Sampling Analysis
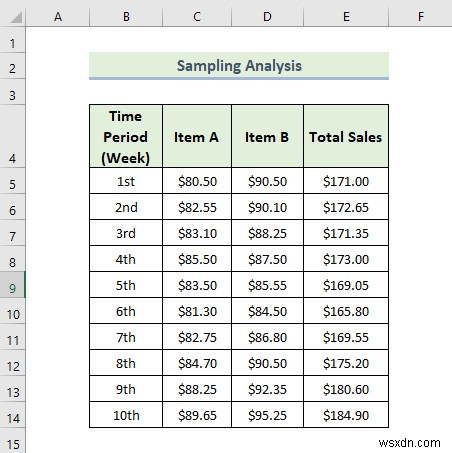
Now, we are going to do a sampling analysis which is one of the best features of the Excel data analysis toolpak. Here, we have a dataset containing two items individual sales and total sales value for different time periods. Let’s walk through the steps to do sampling analysis.
📌 Các bước:
- First, go to the Data tab in the top ribbon.
- Then, select the Data Analysis tool.
- When the Data Analysis window appears, select the Sampling tùy chọn.
- Then, click on OK .
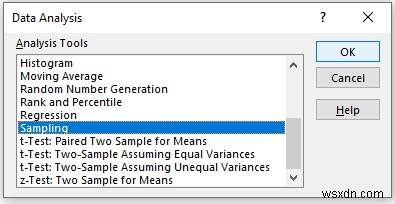
In the Sampling pop-up box,
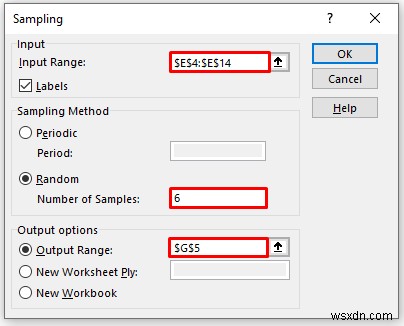
- Provide data in the Input Range box, that you want to calculate the moving average by dragging through the column or row.
- In the Output Range box, provide the data range that you want your calculated data to store by dragging through the column or row. Or you can show the output in the new worksheet by selecting New Worksheet Ply and you can also see the output in the new workbook by selecting New Workbook .
- You have to enter data in the Number of Samples tùy chọn.
- Next, you have to check the Labels if the input data range with the label.
- Then, click on OK .
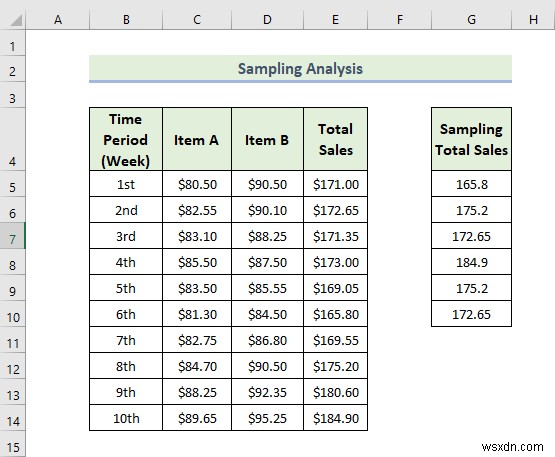
- As a consequence, you will get the following result of the Sampling analysis. In the following picture, we are able to pick up six samples from the Total Sales cột. If you want to pick up more sample data from this column, you have to enter more numbers in the Number of Samples box when the Sampling cửa sổ xuất hiện.
Đọc thêm: How to Analyze Sales Data in Excel (10 Easy Ways)
Kết luận
Đó là phần cuối của phiên hôm nay. Here, we demonstrate thirteen suitable examples to use the data analysis toolpak. I strongly believe that from now, you may be able to use data analysis toolpak in Excel. Nếu bạn có bất kỳ thắc mắc hoặc đề xuất nào, vui lòng chia sẻ chúng trong phần bình luận bên dưới.
Đừng quên kiểm tra trang web Exceldemy.com của chúng tôi cho các vấn đề và giải pháp liên quan đến Excel khác nhau. Tiếp tục học các phương pháp mới và tiếp tục phát triển!
Các bài viết liên quan
- How to Analyze Data in Excel Using Pivot Tables (9 Suitable Examples)
- Analyze Time-Scaled Data in Excel (With Easy Steps)
- How to Analyze Qualitative Data in Excel (with Easy Steps)
- Analyze qPCR Data in Excel (2 Easy Methods)
- How to Analyze Text Data in Excel (5 Suitable Ways)
