Bài viết này minh họa cách thực hiện Phân tích hồi quy trong Excel bằng cách sử dụng công cụ Phân tích dữ liệu và diễn giải Bảng Anova thu được từ các phân tích. Nó được sử dụng rộng rãi trong mô hình thống kê để ước tính tác động của các biến đối với một chủ đề cụ thể được quan tâm. Hãy theo dõi bài viết để biết cách sử dụng công cụ phân tích hồi quy trong excel để thực hiện công việc này.
Bạn có thể tải xuống sách bài tập thực hành từ nút tải xuống bên dưới.
Phân tích hồi quy là gì?
Phân tích hồi quy là một tập hợp các phương pháp được sử dụng để tạo mối quan hệ giữa một biến phụ thuộc và một hoặc nhiều biến độc lập. Hai dạng hồi quy phổ biến nhất là-
- Hồi quy tuyến tính đơn giản
- Hồi quy Nhiều tuyến tính
Hồi quy tuyến tính đơn giản: Bạn có thể thực hiện phân tích này khi chỉ có một biến độc lập ảnh hưởng đến kết quả của biến phụ thuộc. Phương trình hồi quy tuyến tính đơn giản có thể như sau.
Y =α 0 + α 1 X 1 + ϵ
Hồi quy nhiều tuyến tính: Bạn có thể thực hiện phân tích này khi có nhiều biến độc lập ảnh hưởng đến kết quả của biến phụ thuộc. Phương trình cho hồi quy tuyến tính bội có thể như sau.
Y =α 0 + α 1 X 1 + α 2 X 2 +…. + Α n X n + ϵ
Cách thực hiện phân tích hồi quy trong Excel và diễn giải ANOVA
⦿ Phần 1:Cách thực hiện phân tích hồi quy trong Excel
Bạn có thể thực hiện Phân tích hồi quy sử dụng Phân tích dữ liệu công cụ trong Excel. Nhưng bạn có thể cần phải kích hoạt công cụ để có thể truy cập nó. Các bước sau đây sẽ là đủ cho điều đó.
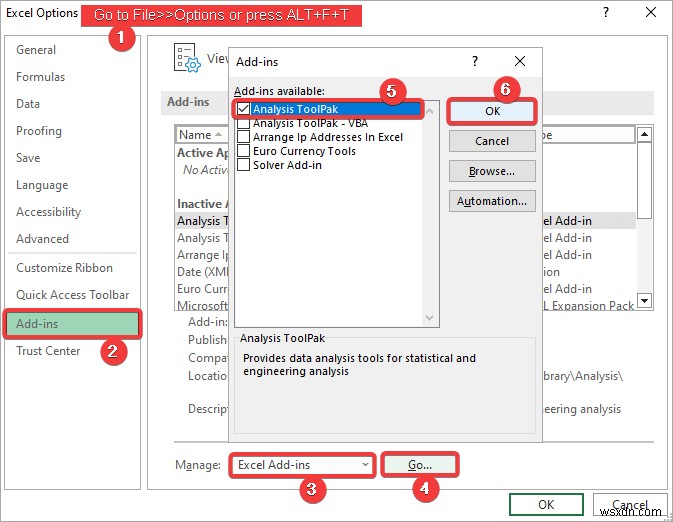
- Đi tới Tệp> > Tùy chọn hoặc nhấn ALT + F + T .
- Chọn Phần bổ trợ tab>> Quản lý Phần bổ trợ Excel >> Đi .
- Kiểm tra Phân tích ToolPak hộp kiểm>> Nhấp vào OK .
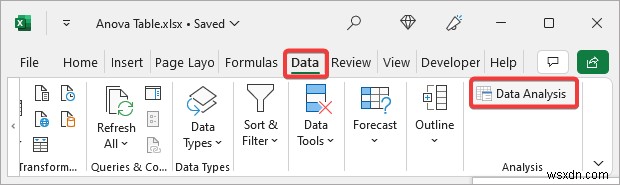
Sau đó, bạn có thể truy cập công cụ Phân tích Dữ liệu từ tab Dữ liệu như được hiển thị bên dưới.
i. Hồi quy tuyến tính đơn giản
Giả sử bạn có tập dữ liệu sau. Đây, X là biến độc lập cho biết lãi suất và Y là biến phụ thuộc cho biết giá nhà. Bạn có thể thực hiện phân tích hồi quy để xem các biến này có liên quan với nhau như thế nào.
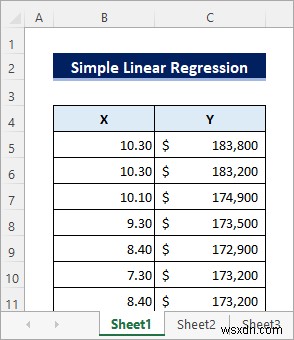
Làm theo các bước bên dưới để thực hiện phân tích Hồi quy tuyến tính đơn giản trên tập dữ liệu trong Excel.
📌 Các bước:
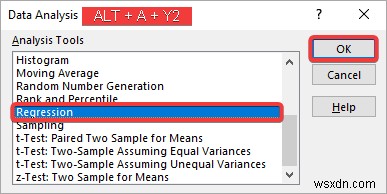
- Đầu tiên, chọn Dữ liệu>> Phân tích Dữ liệu . Sau đó, chọn Hồi quy từ hộp công cụ phân tích và nhấp vào OK.
- Tiếp theo, bạn sẽ thấy Hồi quy hộp thoại. Bây giờ chọn Y các giá trị bao gồm nhãn cho Phạm vi Y đầu vào và X giá trị cho Phạm vi X đầu vào . Sau đó, chọn Nhãn hộp kiểm. Tiếp theo, đánh dấu nút radio cho Phạm vi đầu ra và nhập tham chiếu ô mà bạn muốn nhận kết quả phân tích. Nhấp OK sau đó.
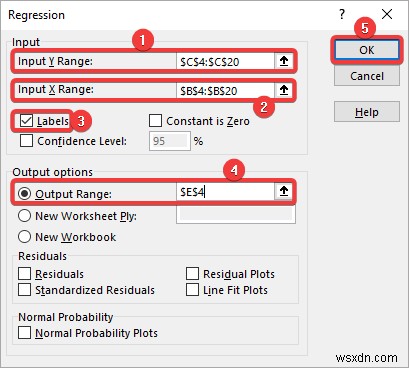
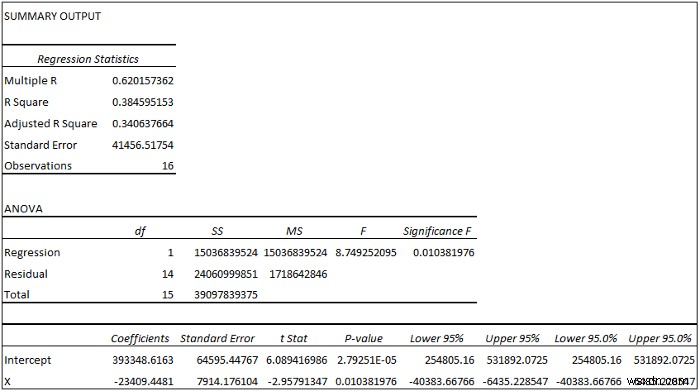
- Cuối cùng, bạn sẽ thấy các kết quả sau ở vị trí đã chỉ định.
ii. Hồi quy nhiều tuyến tính
Bây giờ giả sử bạn có tập dữ liệu sau để thay thế. Đây là Y phụ thuộc biến đại diện cho số lượng người đi hàng tuần ở các thành phố khác nhau. Mặt khác, X độc lập các biến đại diện cho giá mỗi tuần, dân số của các thành phố, thu nhập hàng tháng của người đi xe và tỷ lệ đậu xe trung bình mỗi tháng tương ứng. Bạn có thể xác minh xem các biến độc lập ảnh hưởng như thế nào đến số lượng người đi xe hàng tuần bằng cách thực hiện phân tích hồi quy trên tập dữ liệu.
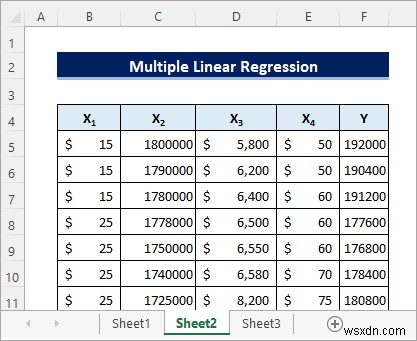
Làm theo các bước bên dưới để thực hiện phân tích hồi quy tuyến tính nhiều trên tập dữ liệu trong Excel cho điều đó.
📌 Các bước:
- Đầu tiên, chọn Dữ liệu>> Phân tích Dữ liệu . Sau đó, chọn Hồi quy từ hộp công cụ phân tích trước đó và nhấp vào OK.
- Tiếp theo, bạn sẽ thấy Hồi quy hộp thoại như trước đó. Bây giờ chọn Y các giá trị bao gồm nhãn cho Phạm vi Y đầu vào và tất cả X giá trị cho Phạm vi X đầu vào . Sau đó, chọn Nhãn hộp kiểm. Tiếp theo, đánh dấu nút radio cho Phạm vi đầu ra . Sau đó, nhập tham chiếu ô mà bạn muốn nhận kết quả phân tích. Nhấp OK sau đó.
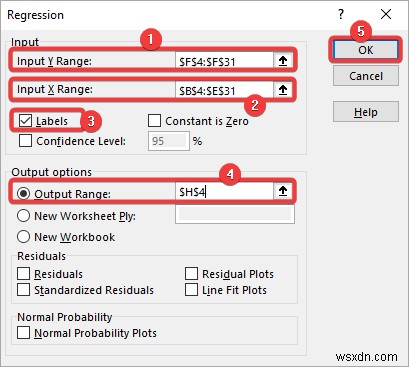
- Cuối cùng, bạn sẽ thấy kết quả sau ở vị trí đã chỉ định.
Bài đọc tương tự
- Cách thực hiện ANOVA hai cách trong Excel (Với các bước đơn giản)
- Biểu đồ Kết quả Anova trong Excel (3 Ví dụ Thích hợp)
- Cách sử dụng ANOVA hai yếu tố với tính năng sao chép trong Excel
- Tính Giá trị P trong Excel ANOVA (3 Ví dụ Thích hợp)
- Cách thực hiện các phép đo lặp lại ANOVA trong Excel (Với các bước đơn giản)
⦿ Phần 2:Cách diễn giải ANOVA và các kết quả phân tích hồi quy khác trong Excel
Kết quả phân tích hồi quy được chia thành ba phần khác nhau như sau.
- Thống kê hồi quy
- Bảng ANOVA
- Bảng Hệ số
Chúng tôi sẽ giải thích ngắn gọn một số thành phần từ mỗi phần vì phần còn lại của chúng không có nhiều tầm quan trọng.
Thống kê hồi quy: Hai giá trị quan trọng trong bảng này là-
- Nhiều R: Nó được gọi là hệ số tương quan. Nó cho bạn biết mối quan hệ tuyến tính mạnh mẽ như thế nào giữa các biến độc lập và phụ thuộc. 1, -1 và 0 cho biết mối quan hệ tương ứng là tích cực, tiêu cực mạnh và không có.
- Hình vuông R: Đây được gọi là hệ số xác định. Nó cho bạn biết tỷ lệ phần trăm của biến phụ thuộc có thể được giải thích bởi (các) biến độc lập. Giá trị gần với 1 chỉ ra rằng sự khác biệt trong biến phụ thuộc có thể được giải thích bằng sự khác biệt trong (các) biến độc lập đối với hầu hết các giá trị.
Bảng ANOVA: Ý nghĩa F là quan trọng nhất ở đây.
- Ý nghĩa F: Giá trị dưới 0 05 cho biết mối quan hệ tuyến tính có ý nghĩa thống kê.
Bảng hệ số: Các hệ số từ bảng này được sử dụng để lập phương trình tuyến tính để biểu thị mối quan hệ giữa các biến.
i. Hồi quy tuyến tính đơn giản
Đầu tiên, hãy quan sát bảng Thống kê hồi quy bên dưới.
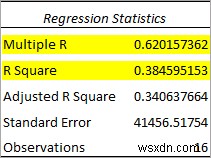
- Nhiều R =0,62 chỉ ra rằng mối quan hệ giữa các biến không quá mạnh nhưng cũng không quá yếu.
- R Square =0,38 cho biết rằng 38% trong tổng số Y giá trị có thể được giải thích bằng X giá trị.
Sau đó, hãy quan sát Bảng ANOVA bên dưới.
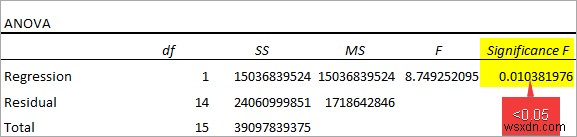
- Ý nghĩa F =0,01 <0,05 chỉ ra rằng mối quan hệ tuyến tính giữa các biến có ý nghĩa thống kê.
Cuối cùng, hãy quan sát bảng Hệ số bên dưới.

Phương trình hồi quy có thể là- Y =393348,62 - 23409.45X + 41456,52.
Đọc thêm: Cách diễn giải kết quả một yếu tố ANOVA trong Excel
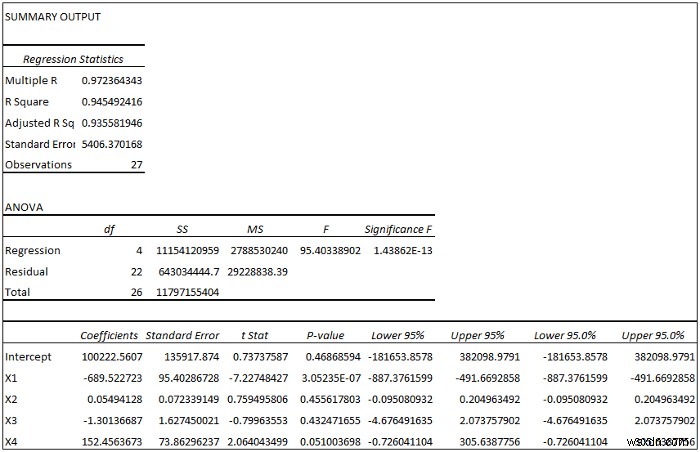
ii. Hồi quy nhiều tuyến tính
Đầu tiên, hãy quan sát bảng Thống kê hồi quy.
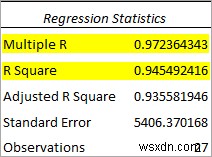
- Nhiều R =0,97 chỉ ra rằng mối quan hệ bền chặt.
- R Square =0,94 cho biết rằng 94% trong tổng số Y giá trị có thể được giải thích bằng X giá trị.
Sau đó, hãy quan sát Bảng ANOVA bên dưới.
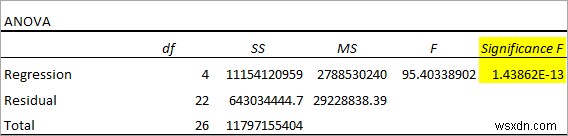
- Ý nghĩa F <<0,05 chỉ ra rằng mối quan hệ tuyến tính giữa các biến có ý nghĩa thống kê cao.
Cuối cùng, hãy quan sát bảng Hệ số bên dưới.
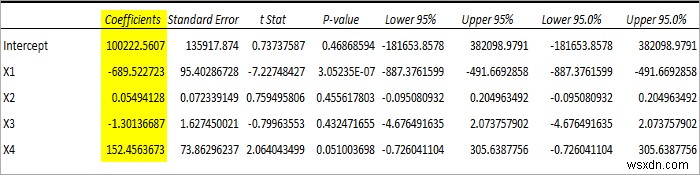
Phương trình hồi quy có thể là- Y =100222,56 - 689,52X 1 + 0,055X 2 - 1,3X 3 + 152.45X 4 + 5406,37 .
Đọc thêm: Cách diễn giải kết quả ANOVA hai chiều trong Excel
Những điều cần nhớ
- Bạn phải bật tiện ích bổ trợ Analysis ToolPak để truy cập vào công cụ Phân tích dữ liệu.
- Đối với Độ tin cậy F, giá trị nhỏ hơn nhiều so với mức độ tin cậy giả định có nghĩa là mối quan hệ bền chặt hơn.
Kết luận
Bây giờ bạn đã biết cách thực hiện phân tích hồi quy trong excel và diễn giải bảng Anova thu được từ phân tích. Bạn có thắc mắc hoặc đề xuất nào thêm không? Hãy cho chúng tôi biết trong phần bình luận bên dưới. Bạn cũng có thể truy cập ExcelDemy của chúng tôi blog để khám phá thêm về excel. Hãy ở lại với chúng tôi và tiếp tục học hỏi.
Các bài viết liên quan
- ANOVA thiết kế khối ngẫu nhiên trong Excel (với các bước dễ dàng)
- Cách sử dụng ANOVA Hai yếu tố mà không cần sao chép trong Excel
- Tạo Bảng ANOVA trong Excel (3 Cách Thích hợp)
- Cách thực hiện ANOVA trong Excel (2 Ví dụ Thích hợp)
- ANOVA Hai chiều trong Excel với Kích thước Mẫu Không bằng nhau (2 Ví dụ)
- Cách thực hiện một cách ANOVA trong Excel (2 Ví dụ Thích hợp)
