Tam giác Reuleaux lớn nhất nội tiếp trong một hình vuông được nội tiếp trong một hình elip?

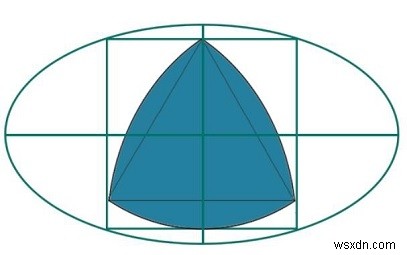
Ở đây chúng ta sẽ thấy diện tích của tam giác Reuleaux lớn nhất nội tiếp trong một hình vuông, hình vuông đó nội tiếp một hình elip. Chúng ta biết rằng độ dài trục chính là 2a và độ dài trục nhỏ là 2b. Cạnh của hình vuông là 'x' và chiều cao của tam giác Reuleaux là h.

Chúng ta biết rằng cạnh của một hình vuông nội tiếp trong một hình elip với trục chính 2a và trục phụ 2b là -

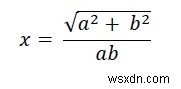
Chiều cao của tam giác Reuleaux bằng a. Vậy h =x. Vậy diện tích tam giác Reuleaux là -

.

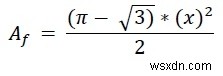Ví dụ

#include <iostream>
#include <cmath>
using namespace std;
float areaReuleaux(float a, float b) { //a and b are half of major and minor axis of ellipse
   if (a < 0 || b < 0) //either a or b is negative it is invalid
      return -1;
   float x = sqrt((a*a) + (b*b)) / (a*b);
   float area = ((3.1415 - sqrt(3)) * (x) * (x))/2;
   return area;
}
int main() {
   float a = 5;
   float b = 4;
   cout << "Area of Reuleaux Triangle: " << areaReuleaux(a, b);
}

Đầu ra

Area of Reuleaux Triangle: 0.0722343