Tam giác Reuleaux lớn nhất nội tiếp trong một hình vuông nội tiếp một elip ở C?

A Tam giác Reuleaux là một hình được hình thành từ giao điểm của ba đĩa tròn, mỗi đĩa có tâm nằm trên ranh giới của hai đĩa kia. Ranh giới của nó là một đường cong có chiều rộng không đổi, đường cong đơn giản nhất và được biết đến nhiều nhất không phải là đường tròn. Chiều rộng không đổi có nghĩa là khoảng cách của mỗi hai đường hỗ trợ song song là như nhau, không phụ thuộc vào hướng của chúng. Bởi vì tất cả các đường kính của nó đều giống nhau.

Ranh giới của một tam giác Reuleaux là một đường cong có chiều rộng không đổi dựa trên một tam giác đều. Tất cả các điểm trên một cạnh đều cách đều với đỉnh đối diện.

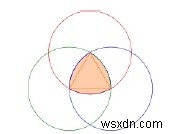
Để tạo tam giác Reuleaux

Công thức cho tam giác Reuleaux

Diện tích của Tam giác Reuleaux, nếu đường cong dựa trên một tam giác đều và cạnh của tam giác là h

A = (π * h2) / 2 – 2 * (Area of equilateral triangle) = (π – √3) * h2 / 2 = 0.70477 * h2

Tam giác Reuleaux lớn nhất nội tiếp trong một hình vuông được nội tiếp trong một hình elip

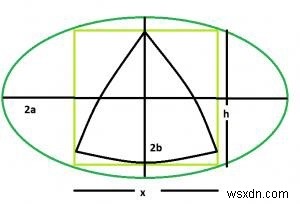
Tam giác Reuleaux lớn nhất nội tiếp trong một hình vuông được nội tiếp trong một hình elip

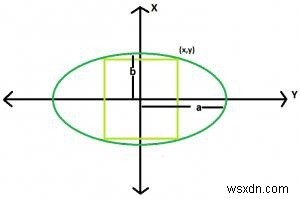
Hình vuông lớn nhất được nội tiếp trong một hình elip

Nếu một hình vuông được nội tiếp trong một hình elip,

Phương trình của hình elip là x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 =1

Nếu, x =y

thì x ^ 2 / a ^ 2 + x ^ 2 / b ^ 2 =1

vì vậy, x =√ (a ^ 2 + b ^ 2) / ab

y =√ (a ^ 2 + b ^ 2) / ab sau đó đến Diện tích, A =4 (a ^ 2 + b ^ 2) / a ^ 2b ^ 2

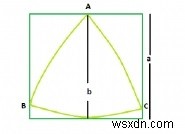
Tam giác Reuleaux lớn nhất trong một hình vuông

Diện tích của Tam giác Reuleaux là 0,70477 * b ² ở đâu b là khoảng cách giữa các đường song song hỗ trợ Tam giác Reuleaux.

khoảng cách giữa các đường song song hỗ trợ Tam giác Reuleaux =Cạnh của hình vuông tức là a

Diện tích Tam giác Reuleaux, A =0,70477 * a ²

Hãy lấy một ví dụ,

Input: a = 5, b = 4
Output: 0.0722389

Giải thích

cạnh của hình vuông nội tiếp trong một hình elip là x =√ (a ^ 2 + b ^ 2) / ab .

tam giác reuleaux, h =x =√ (a ^ 2 + b ^ 2) / ab .

Diện tích của tam giác reuleaux, A =0,70477 * h ^ 2 =0,70477 * ((a ^ 2 + b ^ 2) / a ^ 2b ^ 2) .

Ví dụ

#include <stdio.h>
#include<math.h>
int main() {
   float a = 6, b = 8;
   float h = sqrt(((pow(a, 2) + pow(b, 2))/ (pow(a, 2) * pow(b, 2))));
   float area = 0.70477 * pow(h, 2);
   printf("The area is : %f", area);
   return 0;
}

Đầu ra

The area is : 0.030589