Trong phần này, chúng ta sẽ xem các Đồ thị Eulerian và Hamilton. Nhưng trước khi đi sâu vào vấn đề đó, trước tiên chúng ta phải xem các đường mòn trong biểu đồ là gì. Giả sử chúng ta có một biểu đồ như dưới đây -
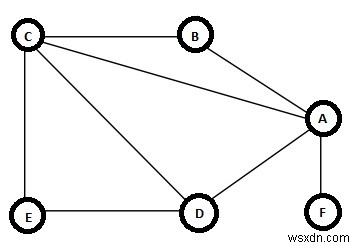
Đường nhỏ là một đường đi, là một chuỗi các cạnh (v1, v2), (v2, v3),…, (vk - 1, vk) trong đó tất cả các đỉnh (v1, v2,…, vk) có thể không phân biệt , nhưng tất cả các cạnh đều khác biệt. Trong ví dụ này, một đường nhỏ là {(B, A), (A, C), (C, D), (D, A), (A, F)} Đây là một đường nhỏ. Nhưng đây sẽ không được coi là đường đi đơn giản vì đỉnh A được thăm hai lần. Nếu đỉnh đầu tiên và đỉnh cuối cùng giống nhau, thì đó sẽ là một đường nhỏ.
Đường mòn Eulerian
Đường mòn Eulerian trong biểu đồ G (V, E) là một đường nhỏ, bao gồm mọi cạnh chính xác một lần. Nếu G đã đóng Eulerian Trail, thì đồ thị đó được gọi là Eulerian Graph. Nói cách khác, chúng ta có thể nói rằng đồ thị G sẽ là đồ thị Eulerian, nếu bắt đầu từ một đỉnh, chúng ta có thể đi qua mọi cạnh chính xác một lần và quay trở lại đỉnh xuất phát. Euler đã chứng minh rằng một đồ thị được gọi là đồ thị Eulerian nếu và chỉ khi mức độ của mọi đỉnh của nó là chẵn.
Chu kỳ Hamilton
Một chu trình được gọi là chu trình Hamilton nếu nó đi qua mọi đỉnh của đồ thị G. Có nhiều định lý khác nhau đưa ra điều kiện đủ để một đồ thị là Hamilton. Tuy nhiên, vấn đề xác định xem một đồ thị tùy ý có phải là Hamilton hay không là vấn đề NPComplete.
