Tìm kiếm đồ thị đầu tiên của Độ sâu cũng tương tự. Nhưng đối với Digraph hoặc đồ thị có hướng, chúng ta có thể tìm thấy một số loại cạnh. Thuật toán DFS tạo thành một cây gọi là cây DFS. Có bốn loại cạnh được gọi là -
-
Cạnh cây (T) - Những cạnh có trong cây DFS
-
Cạnh chuyển tiếp (F) - Song song với một tập hợp các cạnh cây. (Từ số DFS nhỏ hơn đến số DFS lớn hơn và số hoàn thành DFS lớn hơn đến số hoàn thành DFS nhỏ hơn)
-
Cạnh sau (B) - Từ số DFS lớn hơn đến số DFS nhỏ hơn và số hoàn thành DFS nhỏ hơn đến số hoàn thành DFS lớn hơn.
-
Cạnh chéo (C) - Số DFS lớn hơn thành số DFS nhỏ hơn và số hoàn thành DFS lớn hơn thành số hoàn thành DFS nhỏ hơn.
Giả sử chúng ta có một biểu đồ như dưới đây -
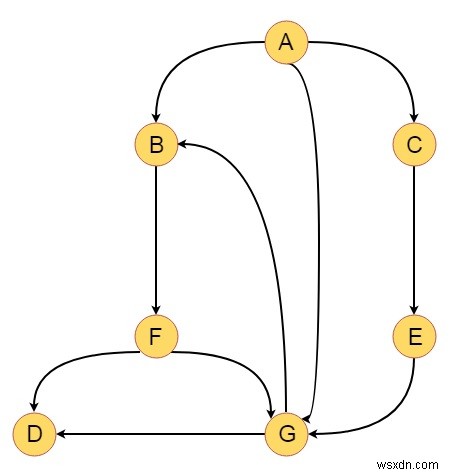
Bây giờ chúng ta sẽ thực hiện DFS bằng cách lấy A làm đỉnh ban đầu, và đặt số DFS và số hoàn thành DFS. Vì vậy, cây sẽ giống như bên dưới -
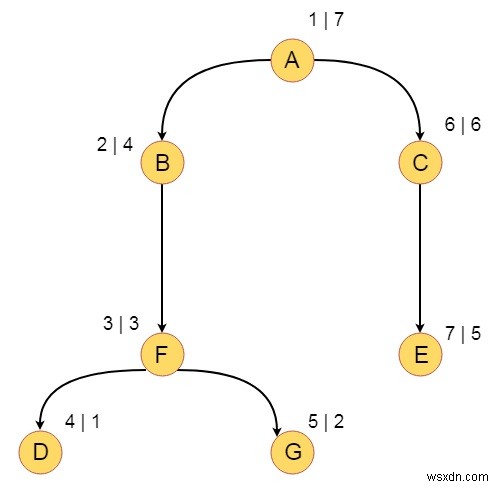
Vì vậy, đường truyền DFS là A, B, F, D, G, C, E
Các cạnh Cây là - T ={(A, B), (B, F), (F, D), (F, G), (A, C), (C, E)}
Các cạnh về phía trước là - F ={(A, G)}
Các cạnh Quay lại là - B ={(G, B)}
Các cạnh chéo là −C ={(G, D)}
