Quadtrees nén
Tại thời điểm lưu trữ mọi nút tương ứng với một ô được chia nhỏ, chúng ta có thể kết thúc việc lưu trữ rất nhiều nút trống. Có thể cắt giảm kích thước của những cây thưa thớt như vậy bằng cách chỉ lưu trữ các cây con mà lá của chúng có dữ liệu thú vị (tức là "các cây con quan trọng"). Một lần nữa, chúng tôi thực sự có thể cắt giảm kích thước hơn nữa. Khi chúng ta chỉ xem xét các cây con quan trọng, quá trình cắt tỉa có thể tránh các đường đi dài trong cây nơi các nút trung gian có bậc hai (liên kết đến một nút cha và một nút con). Hóa ra là chúng ta chỉ yêu cầu lưu trữ nút U ở đầu đường dẫn này (và liên kết một số siêu dữ liệu với nó để đại diện cho các nút đã bị xóa) và đính kèm cây con gốc ở cuối nó vào U. Những cây được nén này vẫn có một chiều cao tuyến tính khi có điểm đầu vào "xấu".
Mặc dù chúng tôi đã cắt bỏ rất nhiều cây khi chúng tôi thực hiện nén này, vẫn có thể đạt được việc chèn, xóa và tìm kiếm theo thời gian logarit bằng cách tận dụng các đường cong bậc Z. Đường cong bậc Z chuyển đổi từng ô của bộ tứ đầy đủ (và do đó thậm chí là cả bộ tứ được nén) trong thời gian O (1) thành đường 1 chiều (và cũng chuyển đổi nó trở lại trong thời gian O (1)), xây dựng một tổng thứ tự trên các phần tử. Bây giờ, chúng ta có thể lưu trữ quadtree trong một cấu trúc dữ liệu cho các tập hợp có thứ tự (trong đó chúng ta lưu trữ các nút của cây). Bây giờ, chúng ta phải nêu một giả định hợp lý trước khi tiếp tục:chúng ta giả sử rằng cho trước hai số thực α, β € [0,1] được ký hiệu là nhị phân, chúng ta có thể tính bằng O (1) thời gian chỉ số của bit đầu tiên mà chúng khác nhau. Chúng tôi cũng giả định rằng chúng tôi có thể tính toán tổ tiên chung nhỏ nhất của hai điểm / ô trong cây phần tư theo thời gian O (1) và thiết lập thứ tự Z tương đối của chúng và chúng ta có thể tính toán hàm sàn trong thời gian O (1). Với những giả định này, vị trí điểm của một điểm Q đã cho (tức là tìm ô chứa Q), các thao tác xóa và chèn đều có thể được thực hiện trong O (n log n) thời gian (tức là thời gian cần thiết để thực hiện tìm kiếm trong cấu trúc dữ liệu tập hợp có thứ tự cơ bản).
Để thực hiện vị trí điểm cho Q (tức là xác định ô của nó trong cây được nén)
- Ô hiện có được tìm thấy trong cây nén đứng trước Q theo thứ tự Z. Gọi ô này là V.
- Nếu Q € V được thực hiện, hãy trả về V.
- Ngoài ra, hãy tìm những gì sẽ là tổ tiên chung nhỏ nhất của điểm Q và ô V trong một bộ tứ không nén. Gọi ô tổ tiên này là U.
- Tìm ô hiện có trong cây đã nén đứng trước U theo thứ tự Z và trả lại ô đó.
Không đi vào chi tiết cụ thể, để thực hiện chèn và xóa, trước tiên chúng ta thực hiện vị trí điểm cho thứ chúng ta muốn chèn / xóa, sau đó chèn / xóa nó. Cần phải cẩn thận để định hình lại cây cho phù hợp, xây dựng và xóa các nút theo yêu cầu.
Octree
Một octree được định nghĩa là cấu trúc dữ liệu dạng cây, trong đó mỗi nút bên trong được liên kết với chính xác tám nút con.
Các bát phân thường được triển khai để phân vùng không gian 3 chiều bằng cách chia nhỏ một cách đệ quy nó thành 8 bát phân.
Các bộ tám được coi là tương tự 3 chiều của các bộ tứ. Tên được tạo từ cây oct +, nhưng lưu ý rằng nó thường được viết "octree" với chỉ một "t".
Octrees thường được triển khai trong đồ họa 3D và công cụ trò chơi 3D.
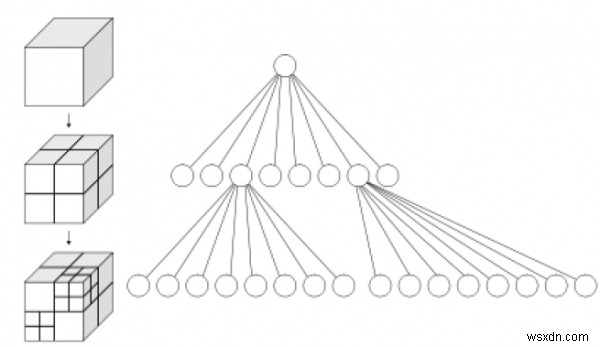
Để biểu diễn không gian
Mỗi nút trong một octa có trách nhiệm chia nhỏ không gian mà nó biểu diễn thành tám octant. Trong một vùng điểm (PR)
octree, nút lưu trữ một điểm 3 chiều rõ ràng, là "trung tâm" của phân khu cho nút đó; quan điểm
chỉ định một trong các góc cho mỗi đứa trẻ trong số tám đứa trẻ. Trong trường hợp octree dựa trên ma trận (MX), điểm chia nhỏ mặc nhiên là tâm của không gian được biểu diễn bởi nút. Nút gốc của một bộ tám PR có thể biểu diễn không gian vô hạn; nút gốc của một bộ tám MX phải có thể đại diện cho một không gian giới hạn hữu hạn để các trung tâm tiềm ẩn được xác định rõ ràng.
Cách sử dụng phổ biến
- Mức độ hiển thị chi tiết trong đồ họa máy tính 3D
- Lập chỉ mục không gian
- Tìm kiếm hàng xóm gần nhất
- Phát hiện va chạm hiệu quả trong không gian ba chiều
- Phân tích phần tử hữu hạn
- Quãng tám voxel thưa thớt
- Ước tính trạng thái
- Ước tính của bộ
