SẮP XẾP QUẢNG CÁO
Adaptive Merge Sort thực hiện việc hợp nhất các danh sách con đã được sắp xếp. Tuy nhiên, kích thước của danh sách con ban đầu phụ thuộc vào sự tồn tại của thứ tự giữa danh sách các phần tử hơn là có danh sách con có kích thước 1. Ví dụ, hãy xem xét danh sách trong hình.
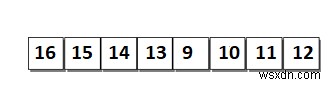
Nó bao gồm 2 danh sách phụ được sắp xếp.
- danh sách con 1 với các phần tử 16,15,14,13.
- danh sách phụ 2 với các phần tử 9,10,11,12.

Danh sách con 1 được sắp xếp nhưng theo thứ tự ngược lại. Do đó, danh sách phụ 1 được đảo ngược như trong hình.

Khi danh sách con được tìm thấy, quá trình hợp nhất sẽ bắt đầu. Sắp xếp hợp nhất thích ứng bắt đầu hợp nhất các danh sách con. Sắp xếp hợp nhất thích ứng sẽ chỉ cần một bước hợp nhất vì chỉ có 2 danh sách con. Kết quả của việc hợp nhất được hiển thị trong hình.

Ý tưởng thiết kế
- Bắt đầu bằng cách tìm các danh sách phụ đã được sắp xếp theo thứ tự bắt buộc hoặc ngược lại
- Nếu tồn tại bất kỳ danh sách con nào có các phần tử theo thứ tự ngược lại, thì hãy đảo ngược danh sách con bằng cách hoán đổi phần tử thứ nhất với phần tử cuối cùng, phần tử thứ 2 với phần tử cuối cùng thứ 2 và nó được tiếp tục.
- Tiếp tục hợp nhất các danh sách phụ để tạo ra các danh sách phụ mới cho đến khi và trừ khi chỉ còn lại 1 danh sách phụ.
Phân tích sắp xếp hợp nhất thích ứng
Sắp xếp hợp nhất thích ứng thay vì bắt đầu bằng danh sách con có kích thước 1, tìm một danh sách con đã được sắp xếp theo thứ tự bắt buộc hoặc ngược lại. Kích thước của danh sách con được tìm thấy ban đầu sẽ là tối thiểu 2 và tối đa là m (m là số phần tử).
Tuy nhiên, nếu danh sách con chứa các phần tử theo thứ tự ngược lại, thì nó sẽ đảo ngược danh sách trước khi bắt đầu thao tác hợp nhất. Việc đảo ngược danh sách yêu cầu (m / 2) hoạt động trao đổi.
Trường hợp tốt nhất
Nếu danh sách đã được sắp xếp theo thứ tự hoặc theo thứ tự ngược lại, thì sắp xếp hợp nhất Thích ứng sẽ chỉ có một danh sách và sẽ không yêu cầu bất kỳ thao tác hợp nhất nào. Tuy nhiên, việc nhận thấy rằng danh sách đã được sắp xếp sẽ yêu cầu thao tác so sánh O (m) và (m / 2) thao tác trao đổi nếu danh sách được sắp xếp theo thứ tự ngược lại. Điều này làm cho sắp xếp Hợp nhất Thích ứng trở nên thích ứng ngay cả khi danh sách được sắp xếp theo thứ tự ngược lại.
Do đó, độ phức tạp về thời gian cho trường hợp tốt nhất được tính như sau -
T(m) = (m-1)+(m/2) T(m) = (2m-2+m)/2 T(m) = O(m).
Tuy nhiên, sắp xếp hợp nhất thích ứng thực hiện thêm không gian O (m) so với sắp xếp hợp nhất
Trường hợp tồi tệ nhất
Sắp xếp hợp nhất thích ứng sẽ tìm danh sách con đã được sắp xếp theo thứ tự bắt buộc hoặc ngược lại. Tuy nhiên, trong trường hợp xấu nhất không có phần tử sắp xếp một phần hoặc toàn bộ. Do đó, danh sách con được tìm thấy ban đầu sẽ có kích thước là 2. Khi danh sách con được tìm thấy, quá trình hợp nhất sẽ bắt đầu.
- hợp nhất các danh sách con có kích thước 2 sẽ tạo ra danh sách con được sắp xếp có kích thước 4.
- hợp nhất các danh sách phụ có kích thước 4 sẽ tạo ra danh sách phụ được sắp xếp có kích thước 8.
- Quá trình hợp nhất tiếp tục cho đến khi và trừ khi 2k
Vì các bước hợp nhất trong trường hợp xấu nhất của Sắp xếp hợp nhất thích ứng cũng giống như sắp xếp hợp nhất. Do đó, Độ phức tạp về thời gian đối với trường hợp xấu nhất của sắp xếp hợp nhất Thích ứng tương tự như sắp xếp hợp nhất -
T(m) = O(m log m).
