Hợp nhất các thuật toán trong cấu trúc dữ liệu

Thuật toán Hợp nhất được sử dụng để hợp nhất hai danh sách đã sắp xếp thành một danh sách. Thuật toán này được sử dụng trong các trường hợp khác nhau. Nếu chúng ta muốn thực hiện sắp xếp hợp nhất, thì chúng ta cần hợp nhất các danh sách sắp xếp thành các danh sách lớn hơn.

Cách tiếp cận rất đơn giản. Chúng tôi lấy hai danh sách, sẽ có hai con trỏ. Cái đầu tiên sẽ trỏ đến phần tử của danh sách nắm tay, cái thứ hai sẽ trỏ đến phần tử của danh sách thứ hai. Dựa trên giá trị của chúng, phần tử nhỏ hơn được lấy từ một trong hai danh sách này, sau đó tăng con trỏ của danh sách tương ứng đó. Thao tác này sẽ được thực hiện cho đến khi hết một danh sách. Sau đó, thêm danh sách còn lại vào cuối danh sách hợp nhất cuối cùng.

Hãy cùng chúng tôi xem hình minh họa để hiểu rõ hơn.

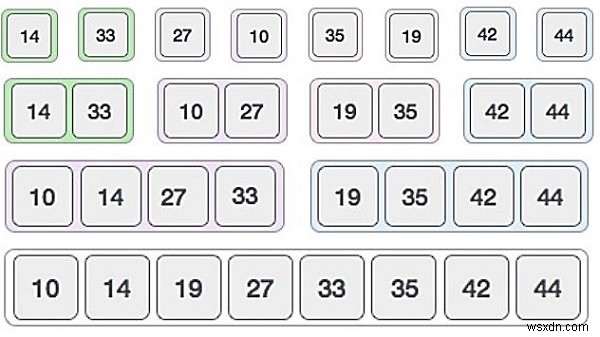
Thuật toán

Hợp nhất (mảng, trái, giữa, phải) -

Begin
   nLeft := m - left+1
   nRight := right – m
   define arrays leftArr and rightArr of size nLeft and nRight respectively
   for i := 0 to nLeft do
      leftArr[i] := array[left +1]
   done
   for j := 0 to nRight do
      rightArr[j] := array[middle + j +1]
   done
   i := 0, j := 0, k := left
   while i < nLeft AND j < nRight do
      if leftArr[i] <= rightArr[j] then
         array[k] = leftArr[i]
         i := i+1
      else
         array[k] = rightArr[j]
         j := j+1
         k := k+1
      done
   while i < nLeft do
      array[k] := leftArr[i]
      i := i+1
      k := k+1
   done
   while j < nRight do
      array[k] := rightArr[j]
      j := j+1
      k := k+1
   done
End