Đồ thị và các thuật toán duyệt của nó

Trong phần này, chúng ta sẽ xem cấu trúc dữ liệu biểu đồ là gì và các thuật toán duyệt của nó.

Biểu đồ là một cấu trúc dữ liệu phi tuyến tính. Đó là bao gồm một số nút và các cạnh được kết nối của chúng. Các cạnh có thể là đạo diễn hoặc vô hướng. Đồ thị này có thể được biểu diễn dưới dạng G (V, E). Biểu đồ sau có thể được biểu diễn dưới dạng G ({A, B, C, D, E}, {(A, B), (B, D), (D, E), (B, C), (C, A )})

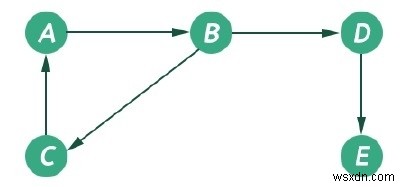
Biểu đồ có hai loại thuật toán duyệt. Chúng được gọi là Tìm kiếm đầu tiên theo chiều rộng và Tìm kiếm đầu tiên theo chiều sâu.

Tìm kiếm đầu tiên theo chiều rộng (BFS)

Duyệt tìm kiếm đầu tiên theo chiều rộng (BFS) là một thuật toán, được sử dụng để truy cập tất cả các nút của một biểu đồ nhất định. Trong thuật toán duyệt này, một nút được chọn và sau đó lần lượt tất cả các nút lân cận được truy cập. Sau khi hoàn thành tất cả các đỉnh liền kề, nó di chuyển tiếp để kiểm tra các đỉnh khác và kiểm tra lại các đỉnh liền kề của nó.

Thuật toán

bfs(vertices, start)
Input: The list of vertices, and the start vertex.
Output: Traverse all of the nodes, if the graph is connected.
Begin
   define an empty queue que
   at first mark all nodes status as unvisited
   add the start vertex into the que
   while que is not empty, do
      delete item from que and set to u
      display the vertex u
      for all vertices 1 adjacent with u, do
         if vertices[i] is unvisited, then
            mark vertices[i] as temporarily visited
            add v into the queue
         mark
      done
      mark u as completely visited
   done
End

Tìm kiếm đầu tiên theo độ sâu (DFS)

Tìm kiếm đầu tiên theo chiều sâu (DFS) là một thuật toán duyệt đồ thị. Trong thuật toán này, một đỉnh bắt đầu được đưa ra và khi một đỉnh liền kề được tìm thấy, nó sẽ di chuyển đến đỉnh liền kề đó trước tiên và cố gắng đi ngang theo cách tương tự.

Thuật toán

dfs(vertices, start)
Input: The list of all vertices, and the start node.
Output: Traverse all nodes in the graph.
Begin
   initially make the state to unvisited for all nodes
   push start into the stack
   while stack is not empty, do
      pop element from stack and set to u
      display the node u
      if u is not visited, then
         mark u as visited
         for all nodes i connected to u, do
            if ith vertex is unvisited, then
               push ith vertex into the stack
               mark ith vertex as visited
         done
   done
End