Cây tìm kiếm nhị phân là cây nhị phân có một số thuộc tính. Các thuộc tính này giống như bên dưới -
- Mỗi cây tìm kiếm nhị phân là một cây nhị phân
- Mọi con bên trái sẽ có giá trị nhỏ hơn giá trị gốc
- Mọi con bên phải sẽ có giá trị lớn hơn giá trị gốc
- Cây tìm kiếm nhị phân lý tưởng sẽ không có cùng một giá trị hai lần.
Giả sử chúng ta có một cây như thế này -
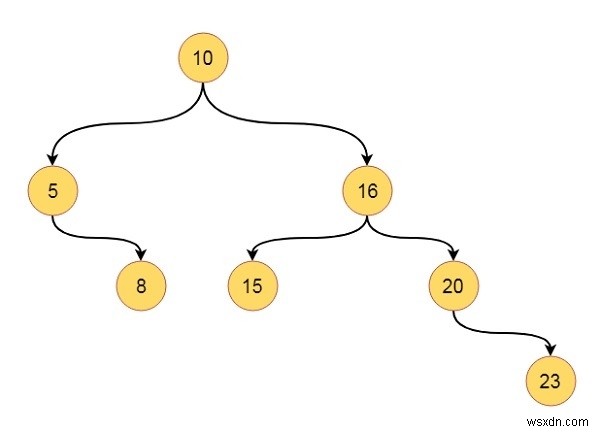
Cây này là một cây tìm kiếm nhị phân. Nó tuân theo tất cả các thuộc tính đã đề cập. Nếu chúng ta chuyển các phần tử vào chế độ duyệt inorder, chúng ta có thể nhận được 5, 8, 10, 15, 16, 20, 23. Hãy xem một đoạn mã để hiểu cách chúng ta có thể triển khai điều này trong mã C ++.
Ví dụ
#include<iostream>
using namespace std;
class node{
public:
int h_left, h_right, bf, value;
node *left, *right;
};
class tree{
private:
node *get_node(int key);
public:
node *root;
tree(){
root = NULL; //set root as NULL at the beginning
}
void inorder_traversal(node *r);
node *insert_node(node *root, int key);
};
node *tree::get_node(int key){
node *new_node;
new_node = new node; //create a new node dynamically
new_node->h_left = 0; new_node->h_right = 0;
new_node->bf = 0;
new_node->value = key; //store the value from given key
new_node->left = NULL; new_node->right = NULL;
return new_node;
}
void tree::inorder_traversal(node *r){
if(r != NULL){ //When root is present, visit left - root - right
inorder_traversal(r->left);
cout << r->value << " ";
inorder_traversal(r->right);
}
}
node *tree::insert_node(node *root, int key){
if(root == NULL){
return (get_node(key)); //when tree is empty, create a node as root
}
if(key < root->value){ //when key is smaller than root value, go to the left
root->left = insert_node(root->left, key);
}else if(key > root->value){ //when key is greater than root value, go to the right
root->right = insert_node(root->right, key);
}
return root; //when key is already present, do not insert it again
}
main(){
node *root;
tree my_tree;
//Insert some keys into the tree.
my_tree.root = my_tree.insert_node(my_tree.root, 10);
my_tree.root = my_tree.insert_node(my_tree.root, 5);
my_tree.root = my_tree.insert_node(my_tree.root, 16);
my_tree.root = my_tree.insert_node(my_tree.root, 20);
my_tree.root = my_tree.insert_node(my_tree.root, 15);
my_tree.root = my_tree.insert_node(my_tree.root, 8);
my_tree.root = my_tree.insert_node(my_tree.root, 23);
cout << "In-Order Traversal: ";
my_tree.inorder_traversal(my_tree.root);
} Đầu ra
In-Order Traversal: 5 8 10 15 16 20 23
