Cây tìm kiếm nhị phân duy nhất trong C ++

Giả sử chúng ta có một số nguyên n, chúng ta phải đếm tất cả các cây tìm kiếm nhị phân có cấu trúc duy nhất lưu trữ các giá trị từ 1 đến n. Vì vậy, nếu đầu vào là 3, thì đầu ra sẽ là 5, như cây sẽ là -

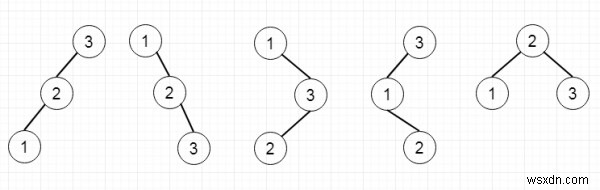
Để giải quyết vấn đề này, chúng ta sẽ làm theo các bước sau -

• tạo một mảng có kích thước n + 1
• dp [0]:=1
• for i:=1 to n
  • cho j:=0 đến i - 1
    • dp [i]:=dp [i] + (dp [i - 1 - j] * dp [j])
• trả về dp [n]

Ví dụ (C ++)

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
   int numTrees(int n) {
      vector <int> dp(n+1);
      dp[0] = 1;
      for(int i =1;i<=n;i++){
         for(int j = 0;j<i;j++){
            //cout << j << " " << i-1-j << " " << j << endl;
            dp[i] += (dp[i-1-j] * dp[j]);
         }
      }
      return dp[n];
   }
};
main(){
   Solution ob;
   cout << ob.numTrees(4);
}

Đầu vào

4

Đầu ra

14