Chúng tôi được cung cấp với chiều cao H của một cây nhị phân. Mục đích là để tìm số lượng / số lượng Cây nhị phân cân bằng có chiều cao nhất định.
Một cây nhị phân - là cấu trúc dữ liệu dạng cây trong đó mỗi nút có nhiều nhất hai nút con, là nút con bên trái và nút con bên phải.
Cây nhị phân cân bằng độ cao - được định nghĩa là một cây nhị phân trong đó độ sâu của hai cây con của mọi nút chỉ khác nhau 1 hoặc 0. Đó là chiều cao của cây con bên trái và cây con bên phải tại mọi nút có hiệu số tối đa là 1.
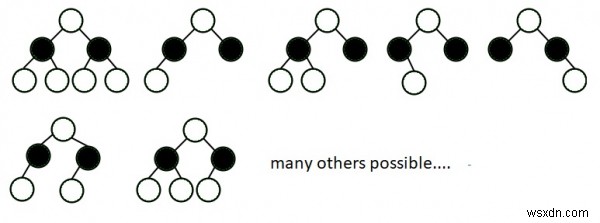
Hình dưới đây chứa các cây nhị phân cân bằng chiều cao có thể có cho chiều cao h =3.
Đầu vào
Height H=2
Đầu ra
Count of Balanced Binary Trees of Height H is : 3
Giải thích - Cho hình bên gồm các cây cân đối có chiều cao H =2

Đầu vào
Height H=3
Đầu ra
Count of Balanced Binary Trees of Height H is : 15
Phương pháp tiếp cận được sử dụng trong chương trình dưới đây như sau
-
Số nguyên H được dùng để biểu thị chiều cao của cây Nhị phân.
-
Hàm countBTheight (int h) lấy chiều cao của cây làm đầu vào và trả về số lượng cây Nhị phân cân bằng có thể có với chiều cao h.
-
Chúng tôi đang sử dụng phương pháp đệ quy.
-
Nếu cây có chiều cao 1, tức là nó chỉ có một nút thì chỉ có một cây với một nút duy nhất là có mặt và cây đó là cân bằng. (if (h ==1), trả về 1)
-
Nếu không thì chiều cao là tổng của cây con trái và phải có chiều cao nhỏ hơn gốc một hoặc hai. (Các cây cân đối có sự khác biệt giữa các chiều cao là 1).
-
Hàm trả về kết quả là số lượng.
Ví dụ
#include <iostream>
int countBTheight(int h){
// One tree is possible with height 0 or 1
if (h == 0 || h == 1)
return 1;
return countBTheight(h-1) * (2 *countBTheight(h-2) + countBTheight(h-1));
}
int main(){
int H = 4;
std::cout << "Count of balanced binary trees of height H is: "<<countBTheight(H);
} Đầu ra
Count of balanced binary trees of height H is: 315
