Giả sử cây nhị phân đầy đủ là cây nhị phân trong đó mỗi nút có đúng 0 hoặc 2 nút con. Vì vậy, chúng ta phải tìm một danh sách tất cả các cây nhị phân đầy đủ có thể có N nút. Mỗi nút của mỗi cây trong câu trả lời phải có node.val =0. Các cây trả về có thể theo thứ tự bất kỳ. Vì vậy, nếu đầu vào là 7, thì cây là -
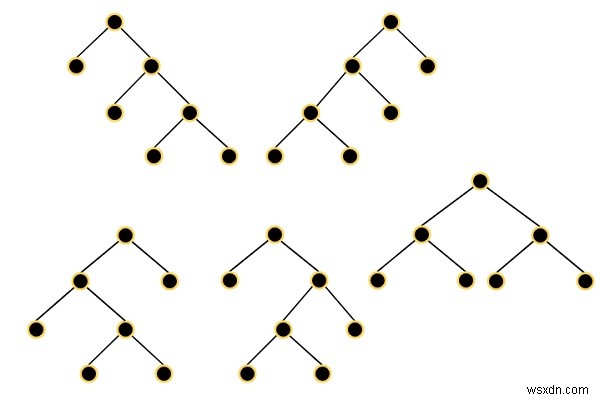
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
-
Xác định một ánh xạ m của khóa kiểu số nguyên và giá trị kiểu cây.
-
xác định một phương thức được gọi là allPossibleFBT (), điều này sẽ nhận N làm đầu vào
-
N là 1, sau đó tạo một cây với một nút có giá trị là 0 và trả về
-
nếu m có khóa N, thì trả về m [N] Xác định một mảng được gọi là temp và req:=N - 1
-
cho bên trái trong phạm vi 1 đến yêu cầu 1
-
right:=req - left
-
nếu left =2 hoặc right =2, thì chuyển sang lần lặp tiếp theo
-
leftPart:=allPossibleFBT (left), rightPart:=allPossibleFBT (right)
-
cho j trong phạm vi 0 đến kích thước của leftPart - 1
-
cho k trong phạm vi 0 đến kích thước của rightPart - 1
-
root:=một nút mới có giá trị 0
-
left of root:=leftPart [j], right of root:=rightPart [k]
-
chèn root vào ans
-
-
-
-
đặt m [N]:=ans và trả về.
Ví dụ (C ++)
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
#include <bits/stdc++.h>
using namespace std;
class TreeNode{
public:
int val;
TreeNode *left, *right;
TreeNode(int data){
val = data;
left = right = NULL;
}
};
void tree_level_trav(TreeNode*root){
if (root == NULL) return;
cout << "[";
queue<TreeNode *> q;
TreeNode *curr;
q.push(root);
q.push(NULL);
while (q.size() > 1) {
curr = q.front();
q.pop();
if (curr == NULL){
q.push(NULL);
} else {
if(curr->left)
q.push(curr->left);
if(curr->right)
q.push(curr->right);
if(curr == NULL || curr->val == 0){
cout << "null" << ", ";
} else {
cout << curr->val << ", ";
}
}
}
cout << "]"<<endl;
}
class Solution {
public:
map < int, vector <TreeNode*> > m;
vector<TreeNode*> allPossibleFBT(int N) {
if(N == 1){
vector <TreeNode*> temp;
TreeNode *n = new TreeNode(1);
n->left = new TreeNode(0);
n->right = new TreeNode(0);
temp.push_back(n);
return temp;
}
if(m.count(N))return m[N];
vector <TreeNode*> ans;
int required = N - 1;
for(int left = 1; left < required; left++){
int right = required - left;
if(left == 2 || right == 2)continue;
vector <TreeNode*> leftPart = allPossibleFBT(left);
vector <TreeNode*> rightPart = allPossibleFBT(right);
for(int j = 0; j < leftPart.size(); j++){
for(int k = 0; k < rightPart.size(); k++){
TreeNode* root = new TreeNode(1);
root->left = leftPart[j];
root->right = rightPart[k];
ans.push_back(root);
}
}
}
return m[N] = ans;
}
};
main(){
vector<TreeNode*> v;
Solution ob;
v = (ob.allPossibleFBT(7)) ;
for(TreeNode *t : v){
tree_level_trav(t);
}
} Đầu vào
7
Đầu ra
[1, 1, 1, null, null, 1, 1, null, null, 1, 1, null, null, null, null, ] [1, 1, 1, null, null, 1, 1, 1, 1, null, null, null, null, null, null, ] [1, 1, 1, 1, 1, 1, 1, null, null, null, null, null, null, null, null, ] [1, 1, 1, 1, 1, null, null, null, null, 1, 1, null, null, null, null, ] [1, 1, 1, 1, 1, null, null, 1, 1, null, null, null, null, null, null, ]
