Chương trình hợp nhất hai cây nhị phân trong C ++

Giả sử chúng ta có hai cây nhị phân và xem xét rằng khi chúng ta đặt một trong số chúng để che đi cây kia, một số nút của hai cây bị chồng lên nhau trong khi các nút khác lại chồng lên nhau. Chúng ta phải hợp nhất chúng thành một cây nhị phân mới. Quy tắc hợp nhất là như vậy nếu hai nút chồng lên nhau, thì tính tổng các giá trị của nút thành giá trị mới của nút đã hợp nhất. Nếu không, nút không trống sẽ được sử dụng làm nút của cây mới.

Vì vậy, nếu cây cối -

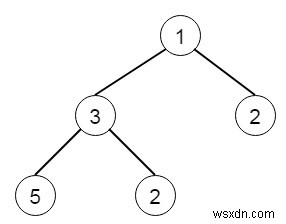
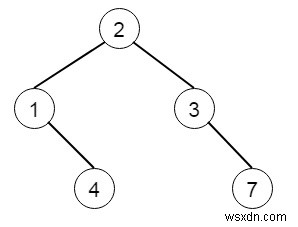
Sau đó, đầu ra sẽ là -

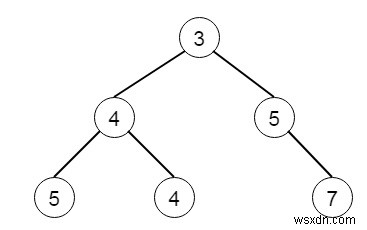
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• Phương thức là giải quyết (). Điều này lấy hai nút cây n1 và n2. Điều này giống như
• nếu n1 trống và n2 khác rỗng thì trả về n2, ngược lại khi n2 trống và n1 khác rỗng thì trả về n1 và khi cả hai đều rỗng thì trả về null
• giá trị của n1:=giá trị của n1 + giá trị của n2
• bên trái của n1:=giải quyết (bên trái của n1, bên trái của n2)
• bên phải của n1:=giải quyết (bên phải của n1, bên phải của n2)
• trả về n1

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

Ví dụ

#include<bits/stdc++.h>
using namespace std;
class TreeNode {
public:
   int val;
   TreeNode *left;
   TreeNode *right;
   TreeNode(int v){
      val = v;
      left = right = NULL;
   }
};
void inord(TreeNode *root) {
   if (root != NULL) {
      inord(root->left);
      cout << root->val << " ";
      inord(root->right);
   }
}
class Solution {
public:
   TreeNode* solve(TreeNode* n1, TreeNode* n2) {
      if(!n1 && n2)
         return n2;
      else if(!n2 && n1)
         return n1;
      else if(!n1 && !n2)
         return NULL;
         n1->val+=n2->val;
         n1->left = solve(n1->left,n2->left);
         n1->right = solve(n1->right,n2->right);
         return n1;
   }
};
main(){
   TreeNode *root1 = new TreeNode(1);
   root1->left = new TreeNode(3);
   root1->right = new TreeNode(2);
   root1->left->left = new TreeNode(5);
   TreeNode *root2 = new TreeNode(2);
   root2->left = new TreeNode(1);
   root2->right = new TreeNode(3);
   root2->left->right = new TreeNode(4);
   root2->right->right = new TreeNode(7);
   Solution ob;
   TreeNode *root_res = ob.solve(root1, root2);
   inord(root_res);
}

Đầu vào

TreeNode *root1 = new TreeNode(1);
root1->left = new TreeNode(3);
root1->right = new TreeNode(2);
root1->left->left = new TreeNode(5);
TreeNode *root2 = new TreeNode(2);
root2->left = new TreeNode(1);
root2->right = new TreeNode(3);
root2->left->right = new TreeNode(4);
root2->right->right = new TreeNode(7);

Đầu ra

5 4 4 3 5 7