Cây con nhỏ nhất với tất cả các nút sâu nhất trong C ++

Giả sử chúng ta có một cây nhị phân bắt nguồn từ gốc, độ sâu của mỗi nút là khoảng cách ngắn nhất đến gốc. Ở đây, một nút là sâu nhất nếu nó có độ sâu lớn nhất có thể trong số bất kỳ nút nào trong toàn bộ cây. Cây con của một nút là nút đó, cộng với tập hợp tất cả các con của nút đó. Chúng ta phải tìm nút có độ sâu lớn nhất sao cho nó chứa tất cả các nút sâu nhất trong cây con của nó. Vì vậy, nếu cây như -

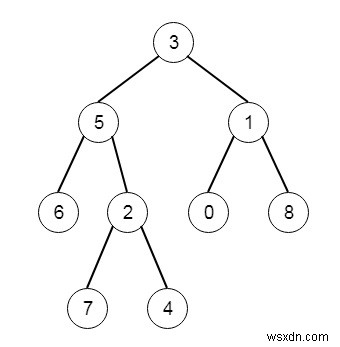
Sau đó, cây con sâu nhất sẽ là -

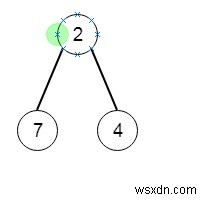
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• Xác định một phương thức có tên là giải quyết (), phương thức này sẽ lấy gốc làm đầu vào

• nếu gốc là null, thì trả về (null, 0)

• l:=giải quyết (bên trái của thư mục gốc), r:=giải quyết (bên phải thư mục gốc)

• nếu giá trị thứ hai của bên trái> giá trị thứ hai của r, thì trả về một cặp (đầu tiên của l, 1 + giây của l)

• ngược lại khi giá trị thứ hai của bên trái

• trả về một cặp (gốc, thứ hai của l + 1)

• Từ phương thức chính, hãy gọi giải quyết (root) và trả về giá trị thứ hai của nó

Ví dụ (C ++)

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

#include <bits/stdc++.h>
using namespace std;
class TreeNode{
   public:
      int val;
      TreeNode *left, *right;
      TreeNode(int data){
         val = data;
         left = right = NULL;
      }
   };
   void insert(TreeNode **root, int val){
      queue<TreeNode*> q;
      q.push(*root);
      while(q.size()){
         TreeNode *temp = q.front();
         q.pop();
         if(!temp->left){
            if(val != NULL)
               temp->left = new TreeNode(val);
            else
               temp->left = new TreeNode(0);
            return;
         } else {
            q.push(temp->left);
         }
         if(!temp->right){
            if(val != NULL)
               temp->right = new TreeNode(val);
            else
               temp->right = new TreeNode(0);
            return;
         } else {
            q.push(temp->right);
      }
   }
}
TreeNode *make_tree(vector<int> v){
   TreeNode *root = new TreeNode(v[0]);
   for(int i = 1; i<v.size(); i++){
      insert(&root, v[i]);
   }
   return root;
}
void tree_level_trav(TreeNode*root){
   if (root == NULL) return;
   cout << "[";
   queue<TreeNode *> q;
   TreeNode *curr;
   q.push(root);
   q.push(NULL);
   while (q.size() > 1) {
      curr = q.front();
      q.pop();
      if (curr == NULL){
         q.push(NULL);
      } else {
         if(curr->left)
         q.push(curr->left);
         if(curr->right)
            q.push(curr->right);
         if(curr->val == 0 || curr == NULL){
            cout << "null" << ", ";
         } else {
            cout << curr->val << ", ";
         }
      }
   }
   cout << "]"<<endl;
}
class Solution {
   public:
   pair <TreeNode*, int> solve(TreeNode* root){
      if(!root || root->val == 0) return {NULL, 0};
      pair <TreeNode*, int> L = solve(root->left);
      pair <TreeNode*, int> R = solve(root->right);
      if(L.second > R.second)return {L.first, L.second + 1};
      else if(L.second < R.second) return {R.first, R.second + 1};
      return {root, L.second + 1};
   }
   TreeNode* subtreeWithAllDeepest(TreeNode* root) {
      return solve(root).first;
   }
};
main(){
   vector<int> v = {3,5,1,6,2,0,8,NULL,NULL,7,4};
   TreeNode *root = make_tree(v);
   Solution ob;
   tree_level_trav(ob.subtreeWithAllDeepest(root)) ;
}

Đầu vào

{3,5,1,6,2,0,8,NULL,NULL,7,4}

Đầu ra

[2,7,4]