Computer >> Máy Tính >  >> Lập trình >> C ++

Tìm thành phố có số lượng hàng xóm ít nhất ở khoảng cách ngưỡng trong C ++

Giả sử có n thành phố được đánh số từ 0 đến n-1. Nếu chúng ta có các cạnh mảng trong đó các cạnh [i] =[fromi, toi, weightti] đại diện cho một cạnh hai chiều và có trọng số giữa các thành phố fromi và toi, và được cung cấp cho ngưỡng khoảng cách là số nguyên. Chúng ta phải tìm thành phố có số lượng thành phố nhỏ nhất có thể đến được qua một số con đường và có khoảng cách nằm ở ngưỡng khoảng cách lớn nhất. Nếu có nhiều hơn một thành phố như vậy, hãy trả về thành phố có số lượng lớn nhất.

Vì vậy, nếu đầu vào giống như -

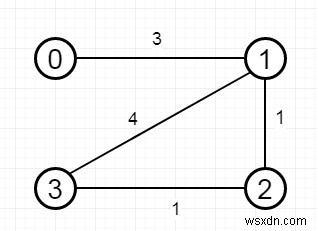
Tìm thành phố có số lượng hàng xóm ít nhất ở khoảng cách ngưỡng trong C ++

n là 4 và ngưỡng khoảng cách cũng là 4, thì đầu ra sẽ là 3. Điều này là do -

Các thành phố lân cận ở ngưỡng khoảng cách =4 cho mỗi thành phố là - 

C0 -> [C1, C2]
C1 -> [C0, C2, C3]
C2 -> [C0, C1, C3]
C3 -> [C1, C2]

Thành phố 0 và 3 có 2 thành phố lân cận ở ngưỡng khoảng cách =4, nhưng chúng tôi phải trả lại thành phố 3 vì nó có số lượng lớn nhất.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

  • Xác định ma trận vuông bậc n x n được gọi là dp và điền giá trị này vào vô cùng

  • tạo ma trận kề (ma trận chi phí) của biểu đồ và lưu trữ vào dp

  • ret:=0 và cnt:=infinity

  • cho k trong phạm vi 0 đến n - 1

    • cho tôi trong phạm vi từ 0 đến n - 1

      • cho j trong phạm vi 0 đến n - 1

        • nếu i =j, thì hãy chuyển sang lần lặp tiếp theo

        • nếu dp [i, j]> dp [i, k] + dp [k, j] thì

          • dp [j, i]:=dp [i, k] + dp [k, j]

          • dp [i, j]:=dp [i, k] + dp [k, j]

  • cho tôi trong phạm vi từ 0 đến n - 1

    • tạm thời:=0

    • cho j trong phạm vi 0 đến n - 1

      • temp:=temp + 1 khi dp [i, j] <=t, nếu không thì tạm thời giữ nguyên

    • nếu temp <=cnt, thì cnt:=temp và ret:=i

  • trả lại ret

Ví dụ (C ++)

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn - 

#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
   int findTheCity(int n, vector<vector<int>>& e, int t) {
      vector < vector <int> > dp(n, vector <int>(n, 1e7));
      for(int i = 0; i < e.size(); i++){
         int u = e[i][0];
         int v = e[i][1];
         int w = e[i][2];
         dp[u][v] = w;
         dp[v][u] = w;
      }
      int ret = 0;
      int cnt = INT_MAX;
      for(int k = 0; k < n; k++){
         for(int i = 0; i < n; i++){
            for(int j = 0; j < n; j++){
               if(i == j) continue;
               if(dp[i][j] > dp[i][k] + dp[k][j]){
                  dp[j][i] = dp[i][j] = (dp[i][k] + dp[k][j]);
               }
            }
         }
      }
      for(int i = 0; i < n; i++){
         int temp = 0;
         for(int j = 0; j < n; j++){
            temp += (dp[i][j] <= t);
         }
         if(temp <= cnt){
            cnt = temp;
            ret = i;
         }
      }
      return ret;
   }
};
main(){
   vector<vector<int>> v = {{0,1,3},{1,2,1},{1,3,4},{2,3,1}};
   Solution ob;
   cout << (ob.findTheCity(4, v, 4));
}

Đầu vào 

4
[[0,1,3],[1,2,1],[1,3,4],[2,3,1]]
4

Đầu ra 

3