Đếm số cây tìm kiếm nhị phân có trong cây nhị phân trong C ++

Chúng tôi được cung cấp một cây nhị phân làm đầu vào. Mục đích là để tìm số cây tìm kiếm nhị phân (BST) hiện diện dưới dạng cây con bên trong nó. BST là một cây nhị phân với con trái nhỏ hơn gốc và con phải nhiều hơn gốc.

Ví dụ

Đầu vào

Cây sẽ được tạo sau khi nhập các giá trị được đưa ra bên dưới -

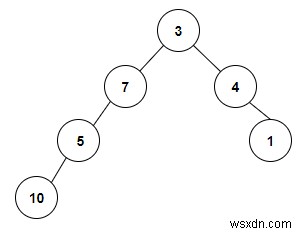
Đầu ra

Count the Number of Binary Search Trees present in a Binary Tree are: 2

Giải thích

chúng ta được cung cấp một mảng các giá trị số nguyên được sử dụng để tạo thành cây nhị phân và chúng ta sẽ kiểm tra xem có cây tìm kiếm nhị phân trong đó hay không. Mỗi nút gốc đại diện cho cây tìm kiếm nhị phân nên trong cây nhị phân đã cho, chúng ta có thể thấy rằng không có cây tìm kiếm nhị phân nào khác hiện diện, do đó số đếm là 2, là tổng số nút lá trong cây nhị phân.

Đầu vào

Cây sẽ được tạo sau khi nhập các giá trị được đưa ra bên dưới -

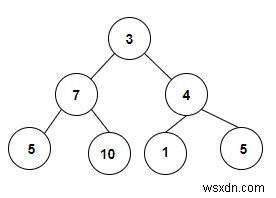
Đầu ra

Count the Number of Binary Search Trees present in a Binary Tree are: 6

Giải thích

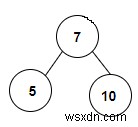
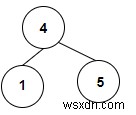
chúng tôi được cung cấp với một mảng các giá trị số nguyên được sử dụng để tạo thành một cây nhị phân và chúng tôi sẽ kiểm tra xem có cây tìm kiếm nhị phân trong đó hay không. Mỗi nút gốc đại diện cho cây tìm kiếm nhị phân vì vậy trong cây nhị phân đã cho, chúng ta có thể thấy rằng có 4 nút lá và hai cây con đang tạo thành BST do đó số lượng là 6.

Phương pháp tiếp cận được sử dụng trong chương trình dưới đây như sau -

Trong cách tiếp cận này, chúng ta sẽ tìm giá trị lớn nhất của nút trong cây con bên trái của nút N và kiểm tra xem nó có nhỏ hơn N. Ngoài ra, chúng ta sẽ tìm giá trị nhỏ nhất trong cây con bên phải của nút N và kiểm tra xem nó có lớn hơn không N. Nếu đúng, thì đó là một BST. Hãy đảo ngược cây nhị phân theo cách từ dưới lên và kiểm tra các điều kiện ở trên và số lượng gia tăng của các BST

• Nút của mọi node_data chứa thông tin như số BSTspresent, giá trị lớn nhất trong cây đó, giá trị nhỏ nhất, boolean true nếu cây con đó là BST.

• Hàm BST_present (struct tree_node * parent) tìm số lượng BST có mặt bên trong cây nhị phân gốc ở gốc.

• Nếu giá trị gốc là NULL thì trả về {0, min, max, true} trong đó min là INT-MIN và max là INT_MAX.

• Nếu các phần tử con bên trái và bên phải là null thì trả về {1, parent−> data, parent−> data, true}

• Đặt node_data Left =BST_present (parent−> left); và node_data Right =BST_present (parent−> right);

• Lấy nút n1 và đặt n1.lowest =min (parent−> data, (min (Left.lowest, Right.lowest))) là thấp nhất trong cây con bên phải của nó.

• Đặt n1.highest =max (parent−> data, (max (Left.highest, Right.highest))); cao nhất trong cây con bên trái của nó.

• nếu (Left.check &&Right.check &&parent−> data> Left.highest &&parent−> data

• Tăng số lượng bsts là n1.total_bst =1 + Left.total_bst + Right.total_bst;

• Nếu không, hãy đặt n1.check =false và tính là n1.total_bst =Left.total_bst + Right.total_bst.

• Cuối cùng, trả về n1.

Ví dụ

#include <bits/stdc++.h>
using namespace std;
struct tree_node{
   struct tree_node* left;
   struct tree_node* right;
   int data;
   tree_node(int data){
      this−>data = data;
      this−>left = NULL;
      this−>right = NULL;
   }
};
struct node_data{
   int total_bst;
   int highest, lowest;
   bool check;
};
node_data BST_present(struct tree_node* parent){
   if(parent == NULL){
      int max = INT_MAX;
      int min = INT_MIN;
      return { 0, min, max, true };
   }
   if(parent−>left == NULL){
      if(parent−>right == NULL){
         return { 1, parent−>data, parent−>data, true };
      }
   }
   node_data Left = BST_present(parent−>left);
   node_data Right = BST_present(parent−>right);
   node_data n1;
   n1.lowest = min(parent−>data, (min(Left.lowest, Right.lowest)));
   n1.highest = max(parent−>data, (max(Left.highest, Right.highest)));
   if(Left.check && Right.check && parent−>data > Left.highest && parent−>data < Right.lowest){
      n1.check = true;
      n1.total_bst = 1 + Left.total_bst + Right.total_bst;
   } else{
      n1.check = false;
      n1.total_bst = Left.total_bst + Right.total_bst;
   }
   return n1;
}
int main(){
   struct tree_node* root = new tree_node(3);
   root−>left = new tree_node(7);
   root−>right = new tree_node(4);
   root−>left−>left = new tree_node(5);
   root−>right−>right = new tree_node(1);
   root−>left−>left−>left = new tree_node(10);
   cout<<"Count the Number of Binary Search Trees present in a Binary Tree are: "<<BST_present(root).total_bst;
   return 0;
}

Đầu ra

Nếu chúng ta chạy đoạn mã trên, nó sẽ tạo ra kết quả sau -

Count the Number of Binary Search Trees present in a Binary Tree are: 2