Cho một đồ thị vô hướng chứa các nút của cây là các đỉnh. Mục đích là để tìm số lượng các nút ở một cấp nhất định của cây bằng cách sử dụng thuật toán BFS (tìm kiếm đầu tiên theo chiều rộng).
Thuật toán BFS:-
Thuật toán này bắt đầu duyệt qua mức đồ thị / cây theo mức độ. Bắt đầu từ nút ở cấp 0, trước tiên nó sẽ đi qua tất cả các nút được kết nối trực tiếp với nó ở cấp 1, sau đó sẽ đi qua tất cả các nút ở cấp tiếp theo, v.v.
- Di chuyển các nút theo chiều ngang ở cấp độ hiện tại.
- Duyệt qua các nút ở cấp độ tiếp theo theo cách tương tự.
Hãy cho chúng tôi hiểu với các ví dụ.
Ví dụ
Đầu vào - cấp =2

Đầu ra - Đếm số nút ở mức đã cho trong cây sử dụng BFS là:1
Giải thích - Như được hiển thị ở trên, tất cả các cấp đều có một nút duy nhất trong biểu đồ.
Đầu vào - cấp =1
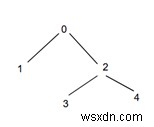
Đầu ra - Đếm số nút ở mức đã cho trong cây sử dụng BFS là:2
Giải thích - Như được hiển thị ở trên, tất cả các cấp đều có một nút duy nhất trong biểu đồ. Các nút là 1, 2.
Phương pháp tiếp cận được sử dụng trong chương trình dưới đây như sau
Trong cách tiếp cận này, chúng ta sẽ duyệt qua từng nút và đặt các cấp của chúng là cấp hơn cha của nó một cấp. Chúng tôi sẽ biểu diễn một biểu đồ bằng cách sử dụng biểu diễn danh sách kề.
Nếu nút bắt đầu là 0 thì
cấp [0] =0,
cấp [1] =cấp [0] +1 =1, cấp [2] =cấp [0] + 1 =1
cấp [3] =cấp [2] +1 =2, cấp [4] =cấp [2] + 1 =2

- Tạo một nút lớp biểu thị một biểu đồ với dữ liệu là số đỉnh và tiếp theo là con trỏ đến danh sách kề.
- Chèn phương thức công khai (int val, int point) thêm cạnh vào biểu đồ.
- Nó thêm val vào danh sách gần kề của điểm và trỏ đến danh sách gần kề của val.
- Hàm count_nodes (int a, int b) trả về số lượng nút ở mức b bắt đầu từ nút nguồn a.
- Đặt số lượng ban đầu là 0.
- Kiểm tra mảng bool =new bool [data].
- Arr mảng [data] lưu trữ mức của mỗi đỉnh của biểu đồ.
- Đặt tất cả các đỉnh của biểu đồ là không được truy cập bằng vòng lặp for và đặt check [i] =false và arr [i] =0.
- Tạo hàng đợi l1 để truyền tải BFS.
- Đánh dấu đỉnh bắt đầu được truy cập là check [a] =true và thêm nó vào l1 bằng cách sử dụng l1.push_back (a) và đặt mức của nó là 0. arr [a] =0.
- Trong khi hàng đợi l1 không trống.
- Lấy phần tử phía trước là a =l1. front () và in nó bằng l1.pop_front ().
- Đánh dấu tất cả các đỉnh chưa đến gần kề của a là đã thăm và thêm vào hàng đợi l1.
- Đặt mức của mỗi đỉnh liền kề là mức của + 1.
- Ở cuối vòng lặp while duyệt qua arr [] bằng cách sử dụng vòng lặp for và cho mỗi số gia tăng arr [i] ==b.
- Kết quả là kết quả trả về cuối kỳ,
Ví dụ
#include <bits/stdc++.h>
using namespace std;
class node {
int data;
list < int > * next;
public:
node(int data) {
this -> data = data;
next = new list < int > [data];
}
void insert(int val, int point) {
next[val].push_back(point);
next[point].push_back(val);
}
int count_nodes(int a, int b);
};
int node::count_nodes(int a, int b) {
int count = 0;
bool * check = new bool[data];
int arr[data];
for (int i = 0; i < data; i++) {
check[i] = false;
arr[i] = 0;
}
list < int > l1;
check[a] = true;
l1.push_back(a);
arr[a] = 0;
while (!l1.empty()) {
a = l1.front();
l1.pop_front();
for (auto it = next[a].begin(); it != next[a].end(); ++it) {
if (!check[ * it]) {
arr[ * it] = arr[a] + 1;
check[ * it] = true;
l1.push_back( * it);
}
}
}
for (int i = 0; i < data; i++) {
if (arr[i] == b) {
count++;
}
}
return count;
}
int main() {
node n1(5);
n1.insert(1, 2);
n1.insert(0, 3);
n1.insert(1, 3);
n1.insert(2, 4);
int level = 1;
cout << "Count of number of nodes at given level in a tree using BFS are: " << n1.count_nodes(0, level);
return 0;
} Nếu chúng ta chạy đoạn mã trên, nó sẽ tạo ra kết quả sau -
Đầu ra
Count of number of nodes at given level in a tree using BFS are: 1
