Chuyển đổi cây nhị phân sang cây tìm kiếm nhị phân trong C ++

A cây nhị phân là một loại cây đặc biệt, trong đó mỗi nút của cây có thể có nhiều nhất hai nút con. Các nút con này được gọi là nút con bên phải và nút con bên trái.

Một cây nhị phân đơn giản là -

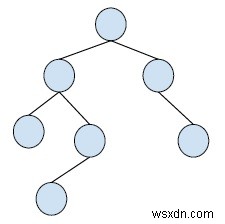
Cây tìm kiếm nhị phân (BST) là một loại cây đặc biệt tuân theo các quy tắc sau -

• Giá trị của nút con bên trái luôn nhỏ hơn Ghi chú gốc

• Nút con bên phải có giá trị lớn hơn nút mẹ.

• tất cả các nút riêng lẻ tạo thành một cây tìm kiếm nhị phân.

Ví dụ về cây tìm kiếm nhị phân (BST) -

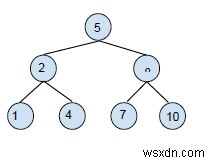
Cây tìm kiếm nhị phân được tạo để giảm độ phức tạp của các hoạt động như tìm kiếm, tìm tối thiểu và tối đa.

Ở đây, chúng ta được cung cấp một cây nhị phân và chúng ta phải chuyển đổi cây nhị phân này thành (BT) sang cây tìm kiếm nhị phân (BST) . Trong quá trình chuyển đổi này, cấu trúc ban đầu của cây nhị phân không được thay đổi.

hãy lấy một ví dụ để hiểu cách chuyển đổi BT thành BST -

Đầu vào -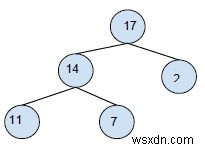

Đầu ra -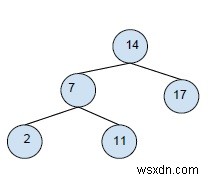

Việc chuyển đổi cây nhị phân sang cây tìm kiếm nhị phân diễn ra bằng ba bước. họ là -

Bước 1 - lưu trữ dữ liệu theo thứ tự của cây nhị phân vào mảng arr [] .

Bước 2 - sắp xếp mảng arr [] bằng bất kỳ kỹ thuật sắp xếp nào.

Bước 3 - Bây giờ, hãy thực hiện việc duyệt inorder của cây và sao chép lần lượt các phần tử của một mảng vào các nút của cây.

Ví dụ

#include<stdio.h>
#include<stdlib.h>
struct node{
   int data;
   struct node *left;
   struct node *right;
};
void Inordertraversal(struct node* node, int inorder[], int *index_ptr){
   if (node == NULL)
      return;
   Inordertraversal(node->left, inorder, index_ptr);
   inorder[*index_ptr] = node->data;
   (*index_ptr)++;
   Inordertraversal(node->right, inorder, index_ptr);
}
int countNodes(struct node* root){
   if (root == NULL)
      return 0;
   return countNodes (root->left) +
   countNodes (root->right) + 1;
}
int compare (const void * a, const void * b){
   return( *(int*)a - *(int*)b );
}
void arrayToBST (int *arr, struct node* root, int *index_ptr){
   if (root == NULL)
      return;
   arrayToBST (arr, root->left, index_ptr);
   root->data = arr[*index_ptr];
   (*index_ptr)++;
   arrayToBST (arr, root->right, index_ptr);
}
struct node* newNode (int data){
   struct node *temp = new struct node;
   temp->data = data;
   temp->left = NULL;
   temp->right = NULL;
   return temp;
}
void printInorder (struct node* node){
   if (node == NULL)
      return;
   printInorder (node->left);
   printf("%d ", node->data);
   printInorder (node->right);
}
int main(){
   struct node *root = NULL;
   root = newNode(17);
   root->left = newNode(14);
   root->right = newNode(2);
   root->left->left = newNode(11);
   root->right->right = newNode(7);
   printf("Inorder Traversal of the binary Tree: \n");
   printInorder (root);
   int n = countNodes(root);
   int *arr = new int[n];
   int i = 0;
   Inordertraversal(root, arr, &i);
   qsort(arr, n, sizeof(arr[0]), compare);
   i = 0;
   arrayToBST (arr, root, &i);
   delete [] arr;
   printf("\nInorder Traversal of the converted BST: \n");
   printInorder (root);
   return 0;
}

Đầu ra

Inorder Traversal of the binary Tree:
11 14 17 2 7
Inorder Traversal of the converted BST:
2 7 11 14 17