Cây tìm kiếm nhị phân (BST) là một loại cây đặc biệt tuân theo các quy tắc sau -
-
Giá trị của nút con bên trái luôn nhỏ hơn Ghi chú gốc
-
nút con bên phải có giá trị lớn hơn nút mẹ.
-
tất cả các nút riêng lẻ tạo thành một cây tìm kiếm nhị phân.
Ví dụ về cây tìm kiếm nhị phân (BST) -

Cây tìm kiếm nhị phân được tạo để giảm độ phức tạp của các hoạt động như tìm kiếm, tìm tối thiểu và tối đa.
Xóa cây tìm kiếm nhị phân (BST)
thao tác xóa đang loại bỏ nút được chỉ định khỏi cây. trong trường hợp xóa các nút, có ba khả năng -
-
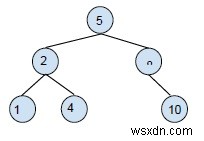
Xóa nút lá khỏi cây:Việc xóa đơn giản nhất là xóa nút lá khỏi cây tìm kiếm nhị phân. Đối với việc xóa nút lá, chỉ lá bị ảnh hưởng. Ví dụ,

xóa nút lá số 7 mang lại,
-
Xóa nút bằng một nút con:đối với việc xóa này, bạn cần thay thế nút con bằng nút cần xóa và sau đó xóa nó. Ví dụ,
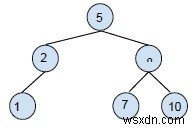
Xóa 2 khỏi BST
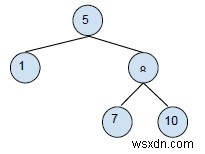
-
Xóa nút có hai nút con:Ở đây nút bị xóa có hai nút con. Vì vậy, chúng tôi sẽ sử dụng trong biểu mẫu thứ tự của cây, ở đây chúng tôi sẽ xóa phần tử và chọn hàng xóm nhỏ hơn của nó cho vị trí của nó và tạo lại phần còn lại. Ví dụ,

Xóa 5 khỏi BST sẽ trả về cây sau.
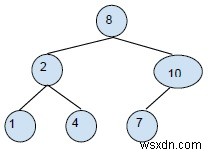
Ví dụ
#include<stdio.h>
#include<stdlib.h>
struct node{
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
void inordertraversal(struct node *root){
if (root != NULL){
inordertraversal(root->left);
printf("%d ", root->key);
inordertraversal(root->right);
}
}
struct node* insert(struct node* node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
struct node * minValueNode(struct node* node){
struct node* current = node;
while (current && current->left != NULL)
current = current->left;
return current;
}
struct node* deleteNode(struct node* root, int key){
if (root == NULL) return root;
if (key < root->key)
root->left = deleteNode(root->left, key);
else if (key > root->key)
root->right = deleteNode(root->right, key);
else{
if (root->left == NULL){
struct node *temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL){
struct node *temp = root->left;
free(root);
return temp;
}
struct node* temp = minValueNode(root->right);
root->key = temp->key;
root->right = deleteNode(root->right, temp->key);
}
return root;
}
int main(){
struct node *root = NULL;
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
printf("Inorder traversal of the given tree \n");
inordertraversal(root);
printf("\nDelete 20\n");
root = deleteNode(root, 20);
printf("Inorder traversal of the modified tree \n");
inordertraversal(root);
printf("\nDelete 30\n");
root = deleteNode(root, 30);
printf("Inorder traversal of the modified tree \n");
inordertraversal(root);
printf("\nDelete 50\n");
root = deleteNode(root, 50);
printf("Inorder traversal of the modified tree \n");
inordertraversal(root);
return 0;
} Đầu ra
Inorder traversal of the given tree 20 30 40 50 60 70 80 Delete 20 Inorder traversal of the modified tree 30 40 50 60 70 80 Delete 30 Inorder traversal of the modified tree 40 50 60 70 80 Delete 50 Inorder traversal of the modified tree 40 60 70 80
