Cây tìm kiếm nhị phân (BST) là một loại cây đặc biệt tuân theo các quy tắc sau -
- giá trị của nút con bên trái luôn nhỏ hơn Ghi chú gốc
- nút con bên phải có giá trị lớn hơn nút mẹ.
- tất cả các nút riêng lẻ tạo thành một cây tìm kiếm nhị phân.
Ví dụ về cây tìm kiếm nhị phân (BST) -

Cây tìm kiếm nhị phân được tạo để giảm độ phức tạp của các hoạt động như tìm kiếm, tìm tối thiểu và tối đa.
Thao tác tìm kiếm trong BST
Thực hiện tìm kiếm trong cây tìm kiếm nhị phân,
Chúng ta cần tìm kiếm chìa khóa trên cây. Đối với điều này, Chúng tôi sẽ so sánh khóa với nút gốc của cây.
Nếu khóa bằng với nút gốc, khóa sẽ được tìm thấy.
Nếu giá trị của khóa lớn hơn nút gốc, hãy lấy cây con bên phải và tìm kiếm khóa.
Nếu giá trị của khóa nhỏ hơn nút gốc, hãy chuyển sang cây con bên trái và tìm kiếm khóa.
Ví dụ
#include<stdio.h>
#include<stdlib.h>
struct node{
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
void traversetree(struct node *root){
if (root != NULL){
traversetree(root->left);
printf("%d \t", root->key);
traversetree(root->right);
}
}
struct node* search(struct node* root, int key){
if (root == NULL || root->key == key)
return root;
if (root->key < key)
return search(root->right, key);
return search(root->left, key);
}
struct node* insert(struct node* node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 23);
insert(root, 15);
insert(root, 12);
insert(root, 17);
insert(root, 32);
insert(root, 29);
insert(root, 45);
printf("The tree is :\n");
traversetree(root);
printf("\nSearching for 12 in this tree ");
if(search(root , 12))
printf("\nelement found");
else
printf("\nelement not found");
return 0;
} Đầu ra
The tree is : 12 15 17 23 29 32 45 Searching for 12 in this tree element found
Thao tác chèn trong BST
Thao tác chèn trong BST diễn ra tại nút lá của cây để chèn chúng ta sẽ bắt đầu so sánh nút đó với nút gốc và tìm vị trí chính xác của nút rồi đặt nó vào. Ví dụ sau sẽ giúp bạn hiểu rõ hơn.

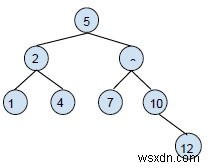
Chèn 12 vào BST này.
Chúng tôi sẽ so sánh nút 12 với nút gốc 12> 5, nó thuộc về cây con bên phải.
So sánh 12 với nút con bên phải 12> 8, nó thuộc quyền của nút con bên phải.
So sánh 12 với con bên phải của cây con bên phải 12> 10, vị trí của nó là bên phải của nút này.
Cây mới được hình thành sẽ là,
Ví dụ
#include<stdio.h>
#include<stdlib.h>
struct node{
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
void traversetree(struct node *root){
if (root != NULL){
traversetree(root->left);
printf("%d \t", root->key);
traversetree(root->right);
}
}
struct node* insert(struct node* node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 23);
insert(root, 15);
insert(root, 12);
insert(root, 17);
insert(root, 32);
insert(root, 29);
printf("The tree is :\n");
traversetree(root);
printf("\nInseting 45 to the tree\n");
insert(root, 45);
printf("Tree after insertion is :\n");
traversetree(root);
return 0;
} Đầu ra
The tree is : 12 15 17 23 29 32 Inserting 45 to the tree Tree after insertion is : 12 15 17 23 29 32 45
