Cân bằng cây tìm kiếm nhị phân trong c ++

Giả sử chúng ta có một cây tìm kiếm nhị phân, chúng ta phải tìm một cây tìm kiếm nhị phân cân bằng với các giá trị nút giống nhau. Cây tìm kiếm nhị phân được cho là cân bằng nếu và chỉ khi độ sâu của hai cây con của mọi nút không bao giờ khác nhau quá 1. Nếu có nhiều hơn một kết quả, hãy trả về bất kỳ kết quả nào trong số chúng. Vì vậy, nếu cây như -

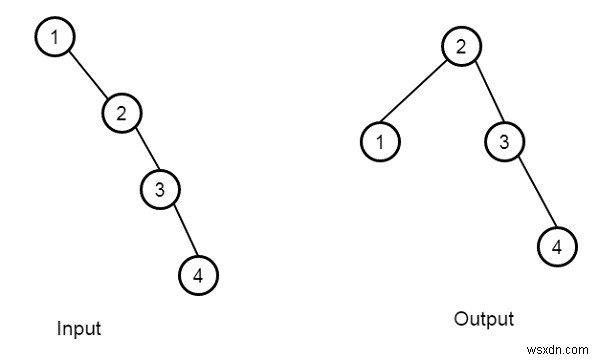
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• Xác định phương thức inorder (), phương thức này sẽ lưu trữ theo trình tự duyệt theo thứ tự thành một mảng

• Xác định phương thức cấu tạo (), phương thức này sẽ có giá trị thấp và cao -

• nếu thấp> cao thì trả về null

• giữa:=low + (cao - thấp) / 2

• root:=nút mới với giá trị arr [mid]

• left of root:=construct (low, mid - 1) và right of root:=construct (mid + 1, high)

• trả về thư mục gốc

• Từ phương thức main, gọi phương thức inorder và trả về cấu trúc (0, size of arr - 1)

Ví dụ (C ++)

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

#include <bits/stdc++.h>
using namespace std;
class TreeNode{
   public:
   int val;
   TreeNode *left, *right;
   TreeNode(int data){
      val = data;
      left = right = NULL;
   }
};
void insert(TreeNode **root, int val){
   queue<TreeNode*> q;
   q.push(*root);
   while(q.size()){
      TreeNode *temp = q.front();
      q.pop();
      if(!temp->left){
         if(val != NULL)
            temp->left = new TreeNode(val);
         else
            temp->left = new TreeNode(0);
         return;
      }else{
         q.push(temp->left);
      }
      if(!temp->right){
      if(val != NULL)
         temp->right = new TreeNode(val);
      else
         temp->right = new TreeNode(0);
      return;
      }else{
         q.push(temp->right);
      }
   }
}
TreeNode *make_tree(vector<int> v){
   TreeNode *root = new TreeNode(v[0]);
   for(int i = 1; i<v.size(); i++){
      insert(&root, v[i]);
   }
   return root;
}
void tree_level_trav(TreeNode*root){
   if (root == NULL) return;
      cout << "[";
      queue<TreeNode *> q;
      TreeNode *curr;
      q.push(root);
      q.push(NULL);
      while (q.size() > 1) {
         curr = q.front();
         q.pop();
         if (curr == NULL){
            q.push(NULL);
      } else {
         if(curr->left)
            q.push(curr->left);
         if(curr->right)
            q.push(curr->right);
         if(curr->val == 0 || curr == NULL){
            cout << "null" << ", ";
         }else{
            cout << curr->val << ", ";
         }
      }
   }
   cout << "]"<<endl;
}
class Solution {
public:
   vector <int> arr;
   void inorder(TreeNode* node){
      if(!node || node->val == 0) return;
      inorder(node->left);
      arr.push_back(node->val);
      inorder(node->right);
   }
   TreeNode* construct(int low, int high){
      if(low > high) return NULL;
      int mid = low + (high - low) / 2;
      TreeNode* root = new TreeNode(arr[mid]);
      root->left = construct(low, mid - 1);
      root->right = construct(mid + 1, high);
      return root;
   }
   TreeNode* balanceBST(TreeNode* root) {
      inorder(root);
      return construct(0, (int)arr.size() - 1);
   }
};
main(){
   vector<int> v = {1,NULL,2,NULL,NULL,NULL,3,NULL,NULL,NULL,NULL,NULL,NULL,NULL,4};
   TreeNode *root = make_tree(v);
   Solution ob;
   tree_level_trav(ob.balanceBST(root));
}

Đầu vào

[1,NULL,2,NULL,NULL,NULL,3,NULL,NULL,NULL,NULL,NULL,NULL,NULL,4]

Đầu ra

[2, 1, 3, 4, ]