Cắt tỉa cây nhị phân trong C ++

Giả sử chúng ta có gốc nút chính của cây nhị phân, trong đó giá trị của mọi nút đều là 0 hoặc 1. Chúng ta phải tìm cùng một cây mà mọi cây con không chứa số 1 đã bị xóa. Vì vậy, nếu cây như -

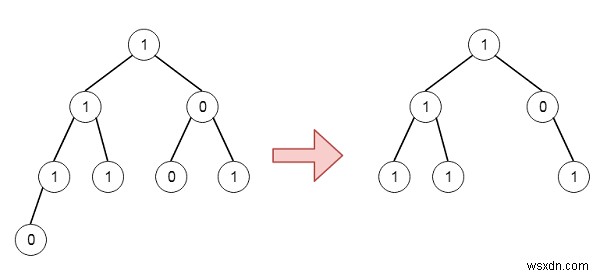
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• Định nghĩa một phương thức đệ quy giải quyết (), điều này sẽ lấy nút. phương pháp sẽ như thế nào -

• Nếu nút là null, thì trả về null

• bên trái của nút:=giải quyết (bên trái của nút)

• bên phải của nút:=giải quyết (bên phải của nút)

• nếu bên trái của nút là null và bên phải của nút cũng là null và giá trị của nút là 0, thì trả về null

• nút trả lại

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

Ví dụ

#include <bits/stdc++.h>
using namespace std;
class TreeNode{
   public:
   int val;
   TreeNode *left, *right;
   TreeNode(int data){
      val = data;
      left = NULL;
      right = NULL;
   }
};
void insert(TreeNode **root, int val){
   queue<TreeNode*> q;
   q.push(*root);
   while(q.size()){
      TreeNode *temp = q.front();
      q.pop();
      if(!temp->left){
         temp->left = new TreeNode(val);
         return;
      }else{
         q.push(temp->left);
      }
      if(!temp->right){
         temp->right = new TreeNode(val);
         return;
      }else{
         q.push(temp->right);
      }
   }
}
TreeNode *make_tree(vector<int> v){
   TreeNode *root = new TreeNode(v[0]);
   for(int i = 1; i<v.size(); i++){
      insert(&root, v[i]);
   }
   return root;
}
void tree_level_trav(TreeNode*root){
   if (root == NULL) return;
   cout << "[";
   queue<TreeNode *> q;
   TreeNode *curr;
   q.push(root);
   q.push(NULL);
   while (q.size() > 1) {
      curr = q.front();
      q.pop();
      if (curr == NULL){
         q.push(NULL);
      } else {
         if(curr->left)
            q.push(curr->left);
         if(curr->right)
            q.push(curr->right);
         if(curr == NULL){
            cout << "null" << ", ";
         }else{
            cout << curr->val << ", ";
         }  
      }
   }
   cout << "]"<<endl;
}
class Solution {
   public:
   TreeNode* pruneTree(TreeNode* node) {
      if(!node)return NULL;
      node->left = pruneTree(node->left);
      node->right = pruneTree(node->right);
      if(!node->left && !node->right && !node->val){
         return NULL;
      }
      return node;
   }
};
main(){
   vector<int> v = {1,1,0,1,1,0,1,0};
   TreeNode *root = make_tree(v);
   Solution ob;
   tree_level_trav(ob.pruneTree(root));
}

Đầu vào

[1,1,0,1,1,0,1,0]

Đầu ra

[1, 1, 0, 1, 1, 1, ]