Computer >> Máy Tính >  >> Lập trình >> C ++

Chiều rộng tối đa của cây nhị phân trong C ++

Giả sử chúng ta có một cây nhị phân, chúng ta phải xác định một hàm để có được chiều rộng lớn nhất của cây đã cho. Ở đây chiều rộng của cây là chiều rộng tối đa giữa tất cả các cấp. Chúng ta sẽ coi cây nhị phân có cấu trúc giống như một cây nhị phân đầy đủ, nhưng một số nút là null. Chiều rộng của một mức thực sự là chiều dài giữa các nút cuối (ngoài cùng bên trái và bên phải hầu hết các nút không rỗng trong mức, nơi các nút rỗng giữa các nút cuối cũng được tính để tính độ dài). Vì vậy, nếu cây như -

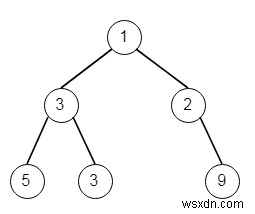
Chiều rộng tối đa của cây nhị phân trong C ++


Sau đó, chiều rộng tối đa là 4, vì các nút của lớp cuối cùng là [5,3, null, 9]

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

  • ans:=1, size:=0

  • xác định một hàng đợi kết thúc kép q nơi chúng ta sẽ lưu trữ cặp (nút, giá trị).

  • insert (root, 1) vào q

  • trong khi q không trống

    • size:=kích thước của q

    • xác định curr cặp (nút, giá trị)

    • nếu kích thước là 1, thì (nút của phần tử phía trước, 1) thành q, xóa phần tử khỏi q

    • trong khi kích thước không phải là 0

      • curr:=phần tử phía trước của q, xóa phần tử phía trước khỏi q

      • nếu bên trái của nút curr không phải là null, thì

        • tạo (bên trái của nút hiện tại, giá trị 2 * của cuộn) và chèn vào q

      • nếu bên phải của nút curr không phải là null, thì

        • tạo (bên phải của nút hiện tại, giá trị 2 * của curr + 1) và chèn vào q

      • nếu kích thước của q> 1, thì

        • ans:=max của ans, giá trị của phần tử cuối cùng trong q - giá trị của phần tử đầu tiên của q + 1

      • size:=size - 1

  • trả lại ans

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

Ví dụ 

#include <bits/stdc++.h>
using namespace std;
class TreeNode{
   public:
   int val;
   TreeNode *left, *right;
   TreeNode(int data){
      val = data;
      left = NULL;
      right = NULL;
   }
};
void insert(TreeNode **root, int val){
   queue<TreeNode*> q;
   q.push(*root);
   while(q.size()){
      TreeNode *temp = q.front();
      q.pop();
      if(!temp->left){
         if(val != NULL)
            temp->left = new TreeNode(val);
         else
            temp->left = new TreeNode(0);
         return;
      }else{
         q.push(temp->left);
      }
      if(!temp->right){
         if(val != NULL)
            temp->right = new TreeNode(val);
         else
            temp->right = new TreeNode(0);
         return;
      }else{
         q.push(temp->right);
      }
   }
}
TreeNode *make_tree(vector<int> v){
      TreeNode *root = new TreeNode(v[0]);
      for(int i = 1; i<v.size(); i++){
      insert(&root, v[i]);
   }
   return root;
}
class Solution {
   public:
   int widthOfBinaryTree(TreeNode* root) {
      int ans = 0;
      deque < pair <TreeNode*, int> > q;
      q.push_back({root,1});
      ans = 1;
      int size;
      while(!q.empty()){
         size = q.size();
         pair <TreeNode*, int> curr;
         if(size == 1){
            q.push_back({q.front().first, 1});
            q.pop_front();
         }
         while(size--){
            curr = q.front();
            q.pop_front();
            if(curr.first->left){
               q.push_back({curr.first->left, 2 * curr.second});
            }
            if(curr.first->right){
               q.push_back({curr.first->right, 2 * curr.second + 1});
            }
         }
         if(q.size() > 1)
            ans = max(ans, q.back().second - q.front().second + 1);
      }
      return ans;
   }
};
main(){
   vector<int> v = {1,3,2,5,3,NULL,9};
   TreeNode *root = make_tree(v);
   Solution ob;
   cout << (ob.widthOfBinaryTree(root));
}

Đầu vào 

[1,3,2,5,3,null,9]

Đầu ra 

4