Trong bài toán này, chúng ta được đưa ra một cây nhị phân. Nhiệm vụ của chúng tôi là tạo một chương trình sẽ tìm tổng xoắn ốc tối đa trong cây nhị phân trong C ++.
Tổng xoắn ốc của cây nhị phân là tổng các nút gặp phải trong chuyển động xoắn ốc của cây nhị phân.
Trong đường xoắn ốc của cây, các nút được truyền từ gốc đến nút lá. Quá trình duyệt diễn ra từ trái sang phải sau đó đối với cấp độ tiếp theo từ phải sang trái và cứ tiếp tục như vậy đối với các cấp độ cao hơn.
Ví dụ -
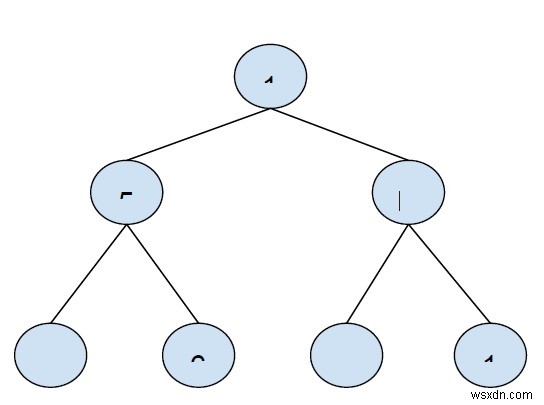
Đầu ra −5
Giải thích -
Chúng tôi sẽ xem xét đường đi qua xoắn ốc cho đến nút đầu tiên của cấp 2 của cây.
1+ 5 = 5.
Tổng các phần tử của hàng thứ ba là (1-9 + 6-4 =-6) sẽ làm giảm tổng tổng thể, do đó nó bị loại bỏ trong khi xem xét tổng lớn nhất.
Để giải quyết vấn đề này, chúng ta sẽ sử dụng một mảng sẽ lưu trữ tổng các phần tử ở mỗi cấp và để tìm tổng tràn ở mỗi cấp, chúng ta sẽ sử dụng hai ngăn xếp. Sau đó, ở phần cuối, chúng tôi sẽ kiểm tra xem việc bao gồm tổng sau cấp làm tăng tổng tối đa hay không, nếu có thì chúng tôi sẽ thực hiện theo cách khác, loại bỏ phần còn lại của vòng xoắn.
Ví dụ
Chương trình tìm tổng xoắn ốc tối đa trong cây nhị phân
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
Node *left, *right;
};
Node* insertNode(int data){
Node* node = new Node;
node->data = data;
node->left = node->right = NULL;
return node;
}
int findMaxSum(vector<int> arr, int n){
int sum = INT_MIN;
int maxSum = INT_MIN;
for (int i = 0; i < n; i++) {
if (sum < 0)
sum = arr[i];
else
sum += arr[i];
maxSum = max(maxSum, sum);
}
return maxSum;
}
int SpiralSum(Node* root){
if (root == NULL)
return 0;
stack<Node*> sRtL;
stack<Node*> sLtR;
vector<int> arr;
sRtL.push(root);
while (!sRtL.empty() || !sLtR.empty()) {
while (!sRtL.empty()) {
Node* temp = sRtL.top();
sRtL.pop();
arr.push_back(temp->data);
if (temp->right)
sLtR.push(temp->right);
if (temp->left)
sLtR.push(temp->left);
}
while (!sLtR.empty()) {
Node* temp = sLtR.top();
sLtR.pop();
arr.push_back(temp->data);
if (temp->left)
sRtL.push(temp->left);
if (temp->right)
sRtL.push(temp->right);
}
}
return findMaxSum(arr, arr.size());
}
int main(){
Node* root = insertNode(1);
root->left = insertNode(5);
root->right = insertNode(-1);
root->left->left = insertNode(-4);
root->left->right = insertNode(6);
root->right->left = insertNode(-9);
root->right->right = insertNode(1);
cout << "Maximum Spiral Sum in binary tree : "<<SpiralSum(root);
return 0;
} Đầu ra
Maximum Spiral Sum in binary tree : 6
