Tìm tổng chiều dọc tối đa trong cây nhị phân trong C ++

Giả sử chúng ta có một cây nhị phân. Nhiệm vụ là in tối đa tổng của tất cả các nút trong trình duyệt theo thứ tự dọc. Vì vậy, nếu cây như dưới đây -

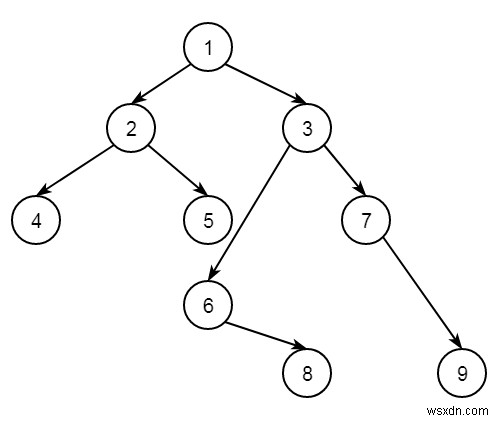
Duyệt theo thứ tự dọc giống như -

4
2
1 + 5 + 6 = 12
3 + 8 = 11
7
9

Ở đây mức tối đa là 12. Cách tiếp cận rất đơn giản. Chúng tôi sẽ thực hiện duyệt theo thứ tự dọc, sau đó tìm tổng và kiểm tra giá trị tối đa.

Ví dụ

#include<iostream>
#include<map>
#include<vector>
#include<queue>
using namespace std;
class Node {
   public:
   int key;
   Node *left, *right;
};
Node* getNode(int key){
   Node* node = new Node;
   node->key = key;
   node->left = node->right = NULL;
   return node;
}
int getMaxSum(Node* root) {
   if (!root)
   return -1;
   int n = 0;
   int k_node = -1;
   map<int, vector<int> > current_map;
   int hd = 0;
   queue<pair<Node*, int> > que;
   que.push(make_pair(root, hd));
   while (!que.empty()) {
      pair<Node*, int> temp = que.front();
      que.pop();
      hd = temp.second;
      Node* node = temp.first;
      current_map[hd].push_back(node->key);
      if (node->left != NULL)
      que.push(make_pair(node->left, hd - 1));
      if (node->right != NULL)
      que.push(make_pair(node->right, hd + 1));
   }
   map<int, vector<int> >::iterator it;
   int maximum = INT_MIN;
   for (it = current_map.begin(); it != current_map.end(); it++) {
      int temp_sum = 0;
      for (int i = 0; i < it->second.size(); ++i) {
         temp_sum += it->second[i];
      }
      if(maximum < temp_sum){
         maximum = temp_sum;
      }
   }
   return maximum;
}
int main() {
   Node* root = getNode(1);
   root->left = getNode(2);
   root->right = getNode(3);
   root->left->left = getNode(4);
   root->left->right = getNode(5);
   root->right->left = getNode(6);
   root->right->right = getNode(7);
   root->right->left->right = getNode(8);
   root->right->right->right = getNode(9);
   cout << "Maximum sum of vertical nodes: " << getMaxSum(root);
}

Đầu ra

Maximum sum of vertical nodes: 12