Tổng đường dẫn tối đa trong cây nhị phân trong C ++

Trong bài toán này, chúng ta được đưa ra một cây nhị phân với mỗi nút chứa một giá trị. Nhiệm vụ của chúng tôi là tạo một chương trình để tìm tổng đường dẫn tối đa giữa hai lá của cây nhị phân.

Ở đây, chúng ta phải tìm dạng đường dẫn từ một nút lá đến một nút lá khác sẽ cung cấp tổng giá trị lớn nhất. Đường dẫn tổng tối đa này có thể / không thể bao gồm nút gốc.

Cây nhị phân là một cấu trúc dữ liệu cây, trong đó mỗi nút có thể có tối đa hai nút con. Chúng được gọi là con trái và con phải.

Ví dụ -

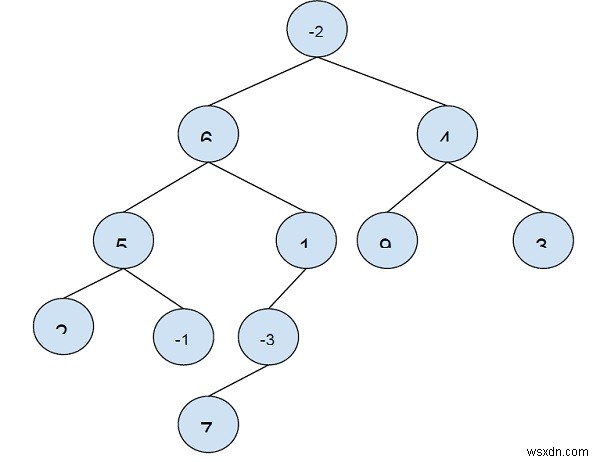
Hãy lấy một ví dụ để hiểu vấn đề -

Đầu vào - // cây nhị phân…

Đầu ra - 24

Giải thích - Đường đi từ nút lá - 2 đến 9 sẽ cho tổng lớn nhất là (2 + 5 + 6 -2 + 4 + 9) =24

Để giải quyết vấn đề này, chúng ta sẽ thực hiện duyệt cây và lưu trữ tổng lớn nhất cho cây con bên trái / cây con bên phải cho nút hiện tại. Ngoài ra, chúng tôi sẽ tìm thấy đường đi tối đa giữa hai nút lá cho đến nay.

Đối với mỗi nút, chúng ta sẽ tìm đường dẫn từ lá đến lá lớn nhất có thể cho các cây con của nó. Và sau đó so sánh nó với đường dẫn tối đa tổng thể và lưu trữ giá trị tối đa của cả hai giá trị trong giá trị tổng đường dẫn tối đa toàn cầu.

Hãy xem giải pháp này từ ví dụ của chúng tôi để hiểu rõ hơn về giải pháp -

Tổng tối đa toàn cục =6 (cho đường dẫn 2 → 5 → -1)

Bây giờ chúng ta sẽ kiểm tra xem có lấy 6 làm nút gốc không.

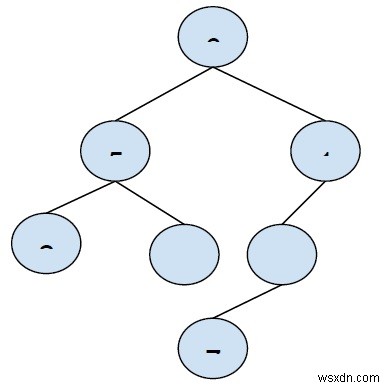
Trong cây con bên trái -

Tổng của đường dẫn đến nút lá là 7 và 4.

Tối đa là 7 (cho đường dẫn 5 → 2).

Trong cây con bên phải -

Tổng của đường dẫn cho đến khi các nút lá là 5 đối với đường dẫn (1rarr; -3rarr; 7), đây là một cách khả thi.

Không, tổng đường dẫn giữa các nút lá là -

Tổng lớn nhất của lá tới gốc (6) trong cây con bên trái + gốc + Tổng lớn nhất cho lá tới gốc (6) trong cây con bên phải =7 + 6 + 5 =18.

So sánh với tổng đường dẫn tối đa toàn cầu (6), Tổng đường dẫn tối đa toàn cầu mới =18.

Ví dụ

Chương trình tìm tổng đường dẫn lớn nhất giữa hai nút lá -

#include <bits/stdc++.h>
using namespace std;
struct Node{
   int data;
   struct Node* left, *right;
};
struct Node* insertNode(int data){
   struct Node* node = new(struct Node);
   node->data = data;
   node->left = node->right = NULL;
   return (node);
}
int max(int a, int b)
{ return (a >= b)? a: b; }
int maxPathSumLeaf(struct Node *root, int &maxSum){
   if (root==NULL) return 0;
   if (!root->left && !root->right) return root->data;
   int leftSubTree = maxPathSumLeaf(root->left, maxSum);
   int rightSubTree = maxPathSumLeaf(root->right, maxSum);
   if (root->left && root->right){
      maxSum = max(maxSum, leftSubTree + rightSubTree + root->data);
      return max(leftSubTree, rightSubTree) + root->data;
   }
   return (!root->left)? rightSubTree + root->data: leftSubTree + root->data;
}
int main(){
   struct Node *root = insertNode(-2);
   root->left = insertNode(6);
   root->right = insertNode(4);
   root->left->left = insertNode(5);
   root->left->right = insertNode(1);
   root->left->left->left = insertNode(2);
   root->left->left->right = insertNode(-1);
   root->left->right->left = insertNode(-3);
   root->left->right->left->left = insertNode(7);
   root->right->left = insertNode(9);
   root->right->right = insertNode(3);
   int maxSum = INT_MIN;
   maxPathSumLeaf(root, maxSum);
   cout<<"Max pathSum of between two leaf nodes for the given binary tree is "<<maxSum;
   return 0;
}

Đầu ra

Max pathSum of between two leaf nodes for the given binary tree is 24