Giả sử chúng ta có một cây nhị phân không rỗng. Chúng ta phải tìm tổng đường dẫn. Vì vậy, ở đây, một đường dẫn là một chuỗi bất kỳ của các nút từ một số nút bắt đầu đến bất kỳ nút nào tại nơi có các kết nối cha-con. Đường dẫn phải chứa ít nhất một nút và không cần đi qua nút gốc. Vì vậy, nếu cây đầu vào là -
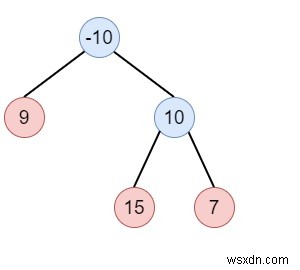
Ở đây đầu ra sẽ là 32.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
-
Xác định một phương thức có tên là giải quyết (), phương thức này sẽ sử dụng nút
-
nếu nút là null hoặc giá trị của nút là 0, thì trả về 0
-
left:=max of 0 và giải quyết (bên trái của nút)
-
right:=max of 0 và giải quyết (bên phải của nút)
-
ans:=max of ans và left + right + data của nút
-
trả về dữ liệu nút + tối đa của trái và phải
-
Từ phương thức chính, đặt ans:=-inf, sau đó gọi giải quyết (root) và trả về ans
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
class TreeNode:
def __init__(self, data, left = None, right = None):
self.data = data
self.left = left
self.right = right
def insert(temp,data):
que = []
que.append(temp)
while (len(que)):
temp = que[0]
que.pop(0)
if (not temp.left):
if data is not None:
temp.left = TreeNode(data)
else:
temp.left = TreeNode(0)
break
else:
que.append(temp.left)
if (not temp.right):
if data is not None:
temp.right = TreeNode(data)
else:
temp.right = TreeNode(0)
break
else:
que.append(temp.right)
def make_tree(elements):
Tree = TreeNode(elements[0])
for element in elements[1:]:
insert(Tree, element)
return Tree
class Solution(object):
def maxPathSum(self, root):
self.ans = -float('inf')
self.solve(root)
return self.ans
def solve(self,node):
if not node or node.data == 0:
return 0
left = max(0,self.solve(node.left))
right = max(0,self.solve(node.right))
self.ans = max(self.ans,left+right+node.data)
return node.data + max(left,right)
ob = Solution()
root = make_tree([-10,9,10,None,None,15,7])
print(ob.maxPathSum(root)) Đầu vào
[-10,9,10,None,None,15,7]
Đầu ra
32
