Bài viết sẽ hướng dẫn bạn cách giải quyết Lập trình tuyến tính kết hợp vấn đề với Excel Solver . Lập trình tuyến tính là một ứng dụng quan trọng khi chúng ta muốn giảm thiểu chi phí hoặc tối đa hóa lợi nhuận trong lĩnh vực kinh doanh. Nó cũng quan trọng đối với cuộc sống hàng ngày của chúng ta vì chúng ta nên tối ưu hóa thói quen ăn uống và các khoản chi tiêu khác. Lập trình tuyến tính kết hợp là một loại Lập trình tuyến tính đặc biệt trong đó lợi nhuận hoặc tối ưu hóa chi phí được tính trên một hoặc nhiều sản phẩm được tạo ra từ hỗn hợp các nguyên liệu thô khác. Chúng tôi sẽ sử dụng Excel để áp dụng Lập trình tuyến tính kết hợp này đến hai ví dụ thực tế để minh họa cách hoạt động của điều này.
Lập trình tuyến tính kết hợp là gì?
Nếu bạn làm việc trong ngành công nghiệp hóa chất hoặc nhà máy thực phẩm, bạn cần tạo ra sản phẩm bằng cách trộn nhiều nguyên liệu khác nhau. Ví dụ, nếu bạn muốn sản xuất một loại thuốc, bạn cần các yếu tố cần thiết cho nó và bạn phải trộn chúng theo một tỷ lệ xác định. Ngoài ra, bạn phải ghi nhớ bạn cần mua bao nhiêu trong số những yếu tố này, chất lượng sản phẩm của bạn như thế nào, v.v. Trong trường hợp này, bạn cần phải tối ưu hóa lượng trộn của các sản phẩm mà bạn muốn cung cấp cho khách hàng. Giải pháp cho vấn đề này được cung cấp bởi Lập trình tuyến tính kết hợp đăng kí. Ứng dụng này giúp chúng tôi học cách sử dụng nguyên liệu thô trong sản xuất.
2 Ví dụ để giải quyết vấn đề lập trình tuyến tính kết hợp với Excel Solver
Trong bài viết này, chúng tôi sẽ giải thích hai loại ví dụ cho Lập trình tuyến tính kết hợp . Một ví dụ là hiển thị cách giải quyết LP kết hợp ( Lập trình tuyến tính ) cho Công thức cố định và cái còn lại dành cho Công thức linh hoạt .
Công thức cố định đề cập đến tình huống mà bạn biết chính xác tỷ lệ hoặc lượng trộn của các vật liệu. Mặt khác, nếu bạn không phải sử dụng một lượng nguyên liệu thô nhất định để sản xuất hàng hóa, thì bạn nên áp dụng LP kết hợp cho Công thức linh hoạt .
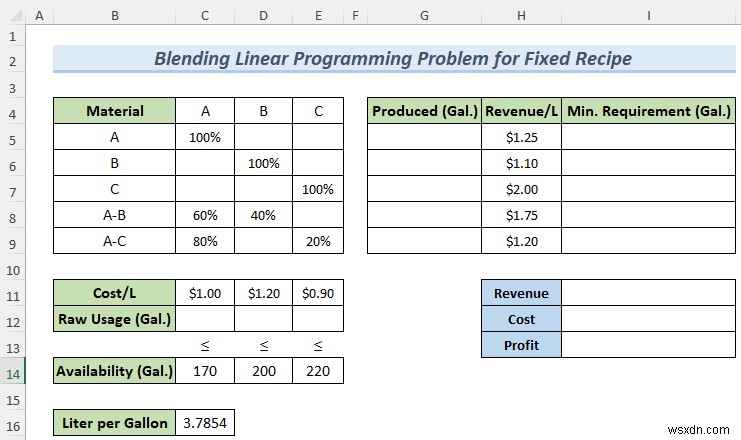
Ví dụ đầu tiên dành riêng để chỉ cho bạn cách giải quyết Công thức cố định vấn đề. Ở đây, chúng tôi có ba loại vật liệu lỏng A , B và C . Chúng tôi sẽ tạo ra hai sản phẩm mới bằng cách sử dụng A-B và A-C với sự kết hợp của 60% -40% và 80% -20% tương ứng. Có các thông số khác như Doanh thu / Lít , Chi phí / Lít , và số lượng nguyên liệu thô có sẵn trong nhà máy. Chúng tôi sẽ tối đa hóa lợi nhuận từ kịch bản này.
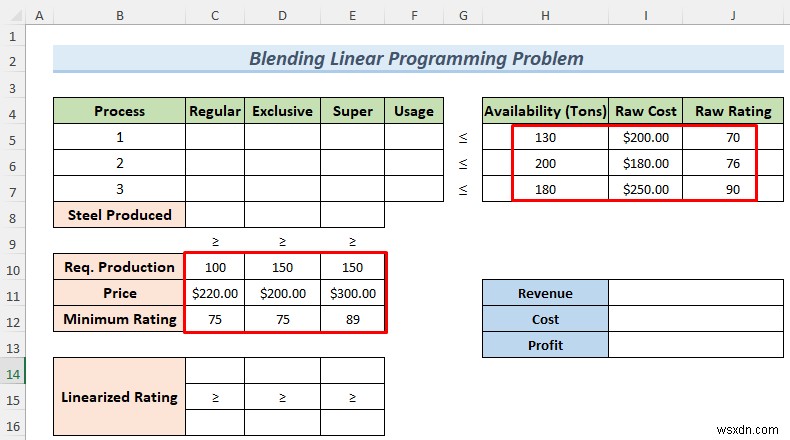
Đối với Công thức linh hoạt vấn đề, chúng tôi sẽ sản xuất các loại thép khác nhau như thông thường , độc quyền và siêu chất lượng thép từ hỗn hợp các nguyên liệu thô khác nhau. Chúng tôi có dữ liệu về lượng nguyên liệu thô có sẵn, chi phí của những nguyên liệu thô này trên mỗi tấn và đánh giá chất lượng của chúng. Chúng tôi cũng đặt số lượng sản xuất cần thiết, giá mỗi tấn thép được sản xuất khác nhau và xếp hạng tối thiểu của chúng. Có một thông số khác mà chúng tôi gọi là Xếp hạng tuyến tính .
1. Lập trình tuyến tính kết hợp cho sự cố công thức cố định
Chúng tôi đã thảo luận vấn đề này trong phần trước. Hãy xem qua quy trình bên dưới.
Các bước:
- Đầu tiên, chúng tôi sẽ thiết lập một số công thức cần thiết. Chúng tôi muốn biết về Cách sử dụng thô của vật liệu và sử dụng công thức sau trong ô C12 để tính toán nó.
=SUMPRODUCT(C5:C9,$G$5:$G$9)
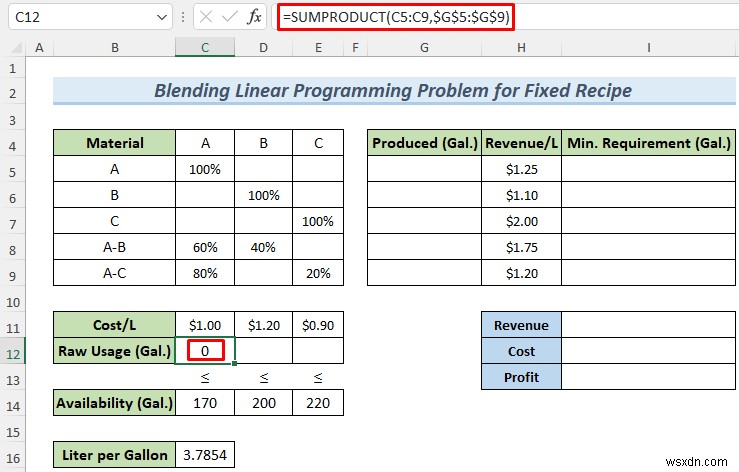
Ở đây, chúng tôi đã sử dụng hàm SUMPRODUCT sẽ trả về Mức sử dụng thô vật liệu A .
- Sau đó, kéo biểu tượng lấp đầy ở bên phải để Tự động điền ô tối đa E12 .
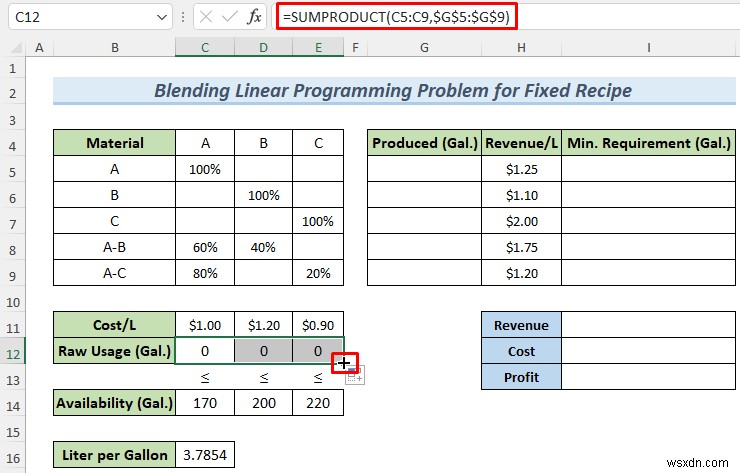
- Sau đó, sử dụng công thức sau trong I11 để tính toán Doanh thu .
=SUMPRODUCT(G5:G9,H5:H9)*C16
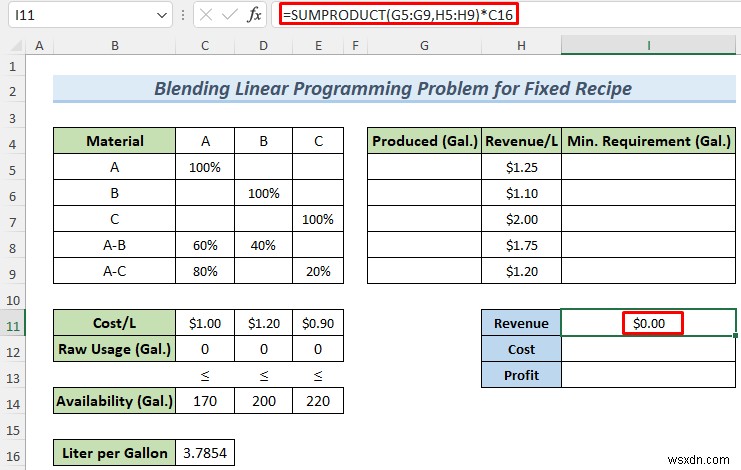
Ở đây, chúng tôi đã nhân công thức với giá trị của ô C16 là 3.7854 bởi vì một gallon bằng 3,7854 Lít.
- Tiếp theo, nhập công thức sau vào ô I12 và nhấn ENTER .
=SUMPRODUCT(C11:E11,C12:E12)*C16
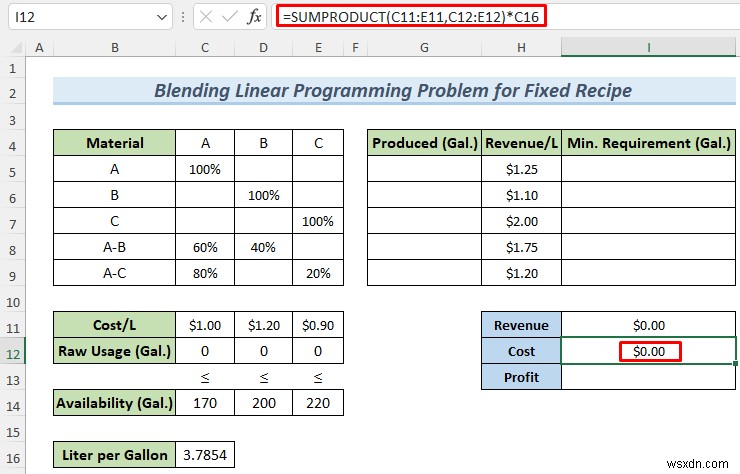
Công thức này sẽ trả lại chi phí sản xuất.
- Sau đó, chúng tôi áp dụng công thức sau để tính lợi nhuận .
=I11-I12
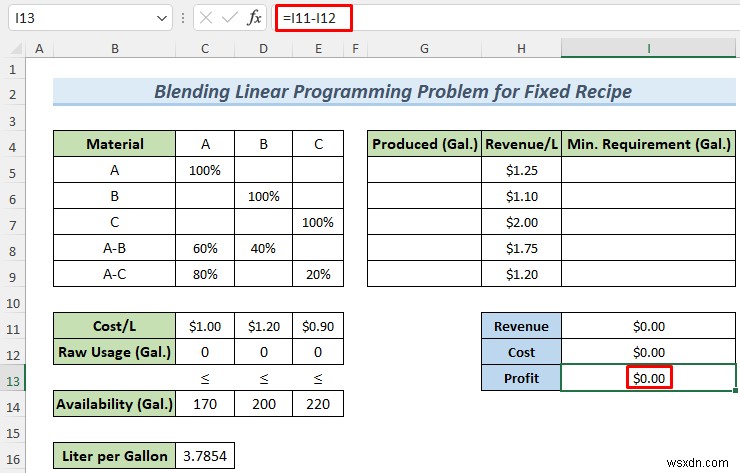
- Bây giờ, hãy đặt yêu cầu sản xuất tối thiểu của bạn.
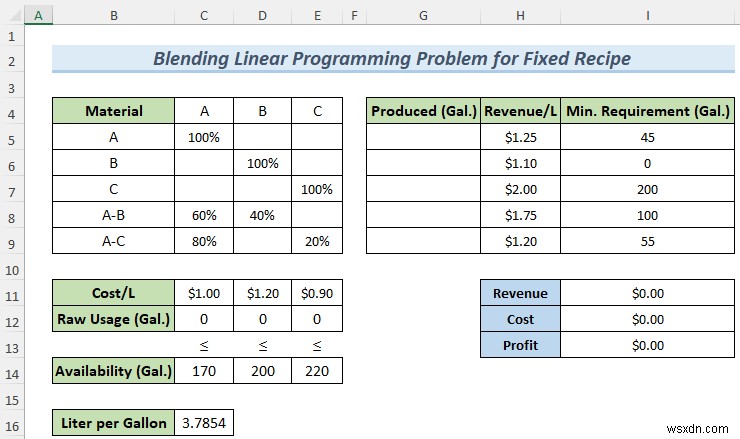
- Sau đó, chuyển đến Dữ liệu >> Người giải quyết . Nếu bạn không biết cách thêm Phần bổ trợ của trình giải quyết trong Tab Dữ liệu , chọn Tệp >> Tùy chọn >> Phần bổ trợ >> Phần bổ trợ Excel >> Đi >> Tiện ích bổ sung của trình giải quyết và nhấp vào OK hoặc theo Liên kết này .
- Để mở Phần bổ trợ của Trình giải quyết , đi tới Dữ liệu >> Người giải quyết .
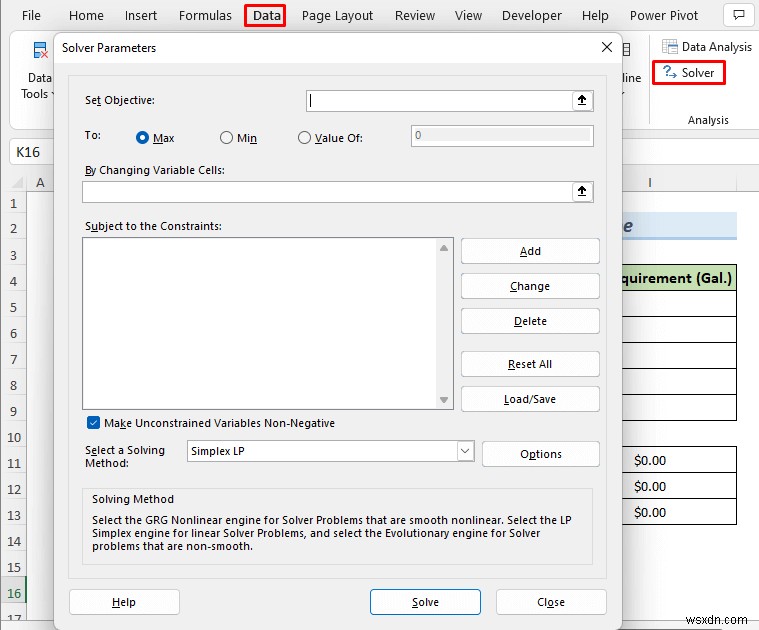
- Chúng tôi muốn tối đa hóa lợi nhuận của mình, vì vậy chúng tôi đặt tham chiếu khách quan là I13 nơi chúng tôi đã lưu trữ Lợi nhuận
- Ngoài ra, biến số của chúng tôi là tỷ lệ pha trộn của các sản phẩm. Vì vậy, chúng tôi đã thêm G5:G9 phạm vi thành ‘ Bằng cách thay đổi ô biến Phần '.
- Sau đó, nhấp vào Thêm để thêm các ràng buộc .
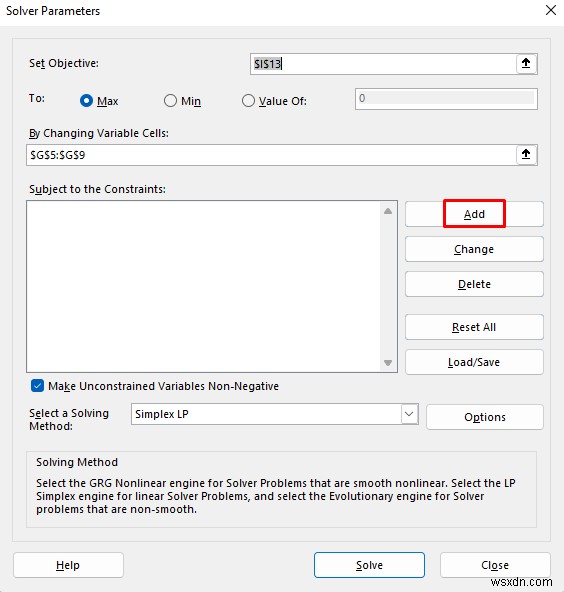
- Cách sử dụng Nguyên liệu thô không được vượt quá Vật liệu có sẵn Vì vậy, hạn chế đầu tiên của chúng tôi là phạm vi C12:E12 sẽ nhỏ hơn hoặc bằng C14:E14 .
- Sau đó, nhấp vào Thêm .
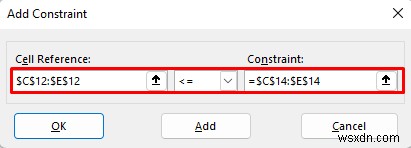
- Tương tự, chúng tôi đã thêm một hạn chế khác ngụ ý rằng số lượng sản xuất lớn hơn số lượng sản xuất yêu cầu tối thiểu.
- Tiếp theo, nhấp vào OK .
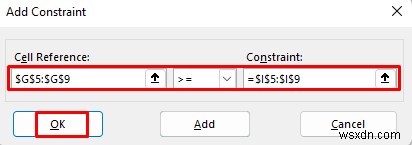
- Sau đó, chọn ‘ Đặt biến không bị ràng buộc thành biến không phủ định '.
- Sau đó, chọn Simplex LP làm Phương pháp giải quyết .
- Sau đó, nhấp vào Giải quyết .
- Sau đó, một hộp thông báo xác nhận sẽ xuất hiện. Chỉ cần nhấp vào OK .
- Cuối cùng, bạn sẽ nhận được giá trị của bao nhiêu Nguyên liệu thô bạn nên sử dụng để nhận được Lợi nhuận tối đa .
- Ngoài ra, bạn cũng sẽ nhận được kết quả về Doanh thu , Chi phí sản xuất và Lợi nhuận
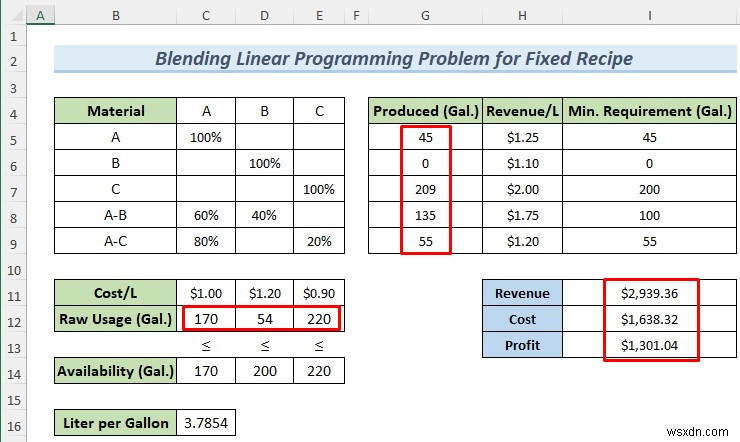
Do đó, bạn có thể giải quyết Lập trình tuyến tính kết hợp sự cố với Trình giải quyết Excel cho Công thức cố định .
2. Excel Solver cho vấn đề lập trình tuyến tính pha trộn công thức linh hoạt
Trong phần này, tôi sẽ chỉ cho bạn cách giải quyết Sự cố lập trình tuyến tính kết hợp cho Công thức linh hoạt . Để biết về sự cố này, vui lòng truy cập liên kết này của bài báo này. Bây giờ, hãy xem qua mô tả sau.
Các bước:
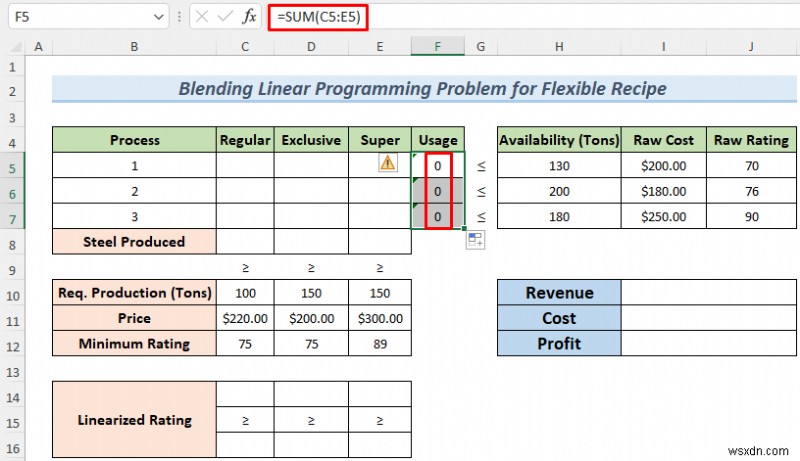
- Đầu tiên, chúng tôi sẽ thiết lập một số công thức cho giải pháp của chúng tôi. Nhập công thức sau vào ô F5 và nhấn ENTER
=SUM(C5:E5)
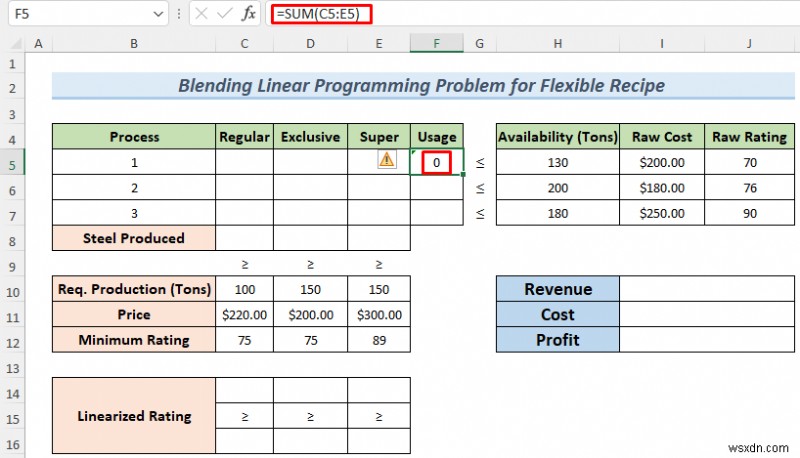
Công thức sử dụng hàm SUM để tính tổng số tiền của loại 1 Thép ( Thông thường , Độc quyền và Super ) sẽ được sản xuất từ Có sẵn đầu tiên tài nguyên.
- Tiếp theo, kéo Tô biểu tượng bên dưới để điền vào các ô lên đến F7 .
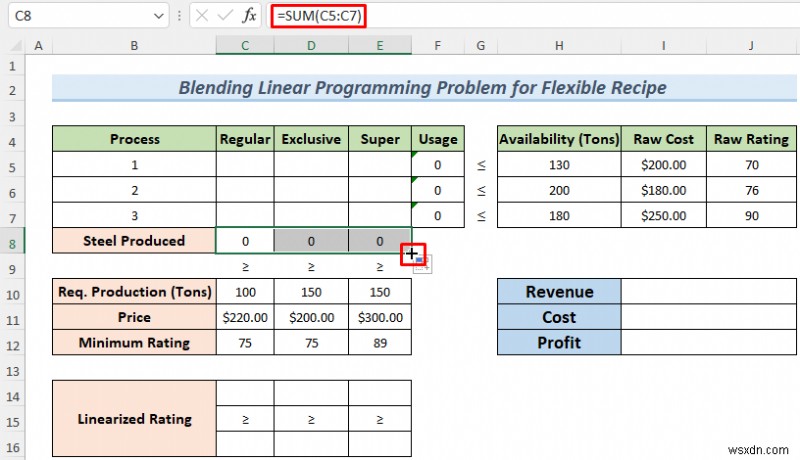
- Sau đó, nhập công thức sau để tính tổng số Thép thông thường số lượng sản xuất.
=SUM(C5:C7)
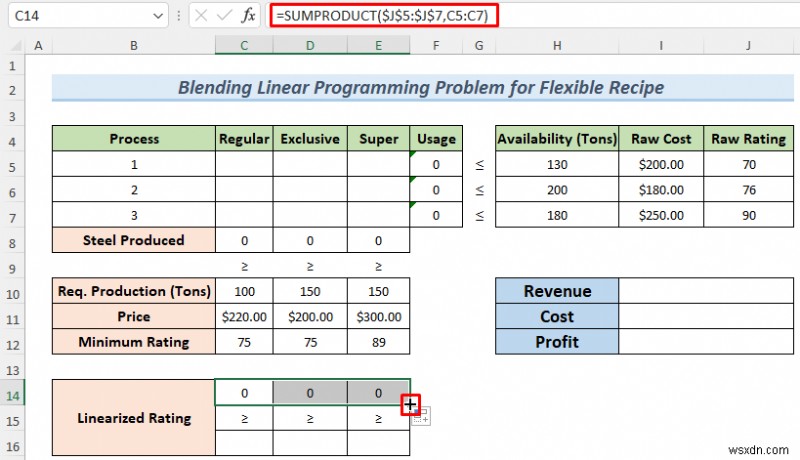
- Tương tự, hãy viết công thức bên dưới vào ô C14 để tính toán Xếp hạng tuyến tính và điền vào các ô liền kề lên đến E14 .
=SUMPRODUCT($J$5:$J$7,C5:C7)
- After that, type the following formula C16 and fill the cells up to E16 .
=C12*C8
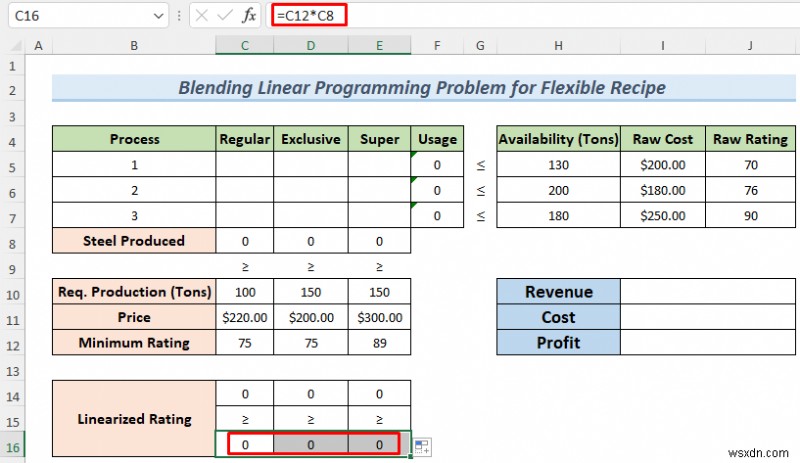
The formula will give us the Linearized Rating of the produced Steels .
- Next, write down the formula below in cell I10 to determine the Revenue .
=SUMPRODUCT(C11:E11,C8:E8)
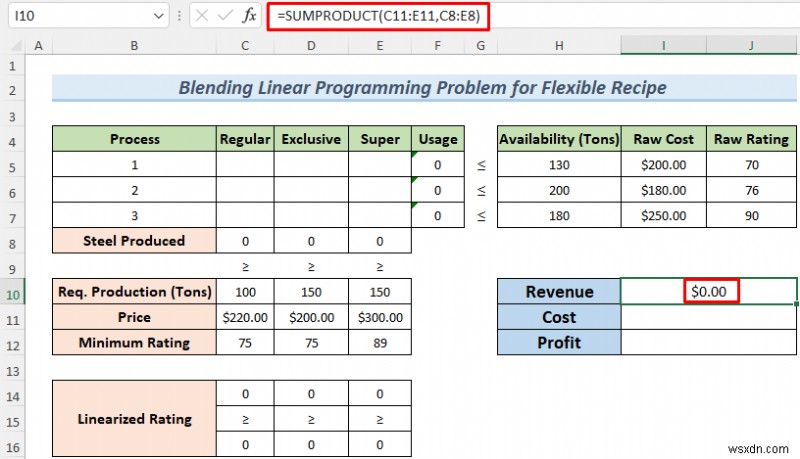
- To calculate the production cost, use the following formula.
=SUMPRODUCT(I5:I7,F5:F7)
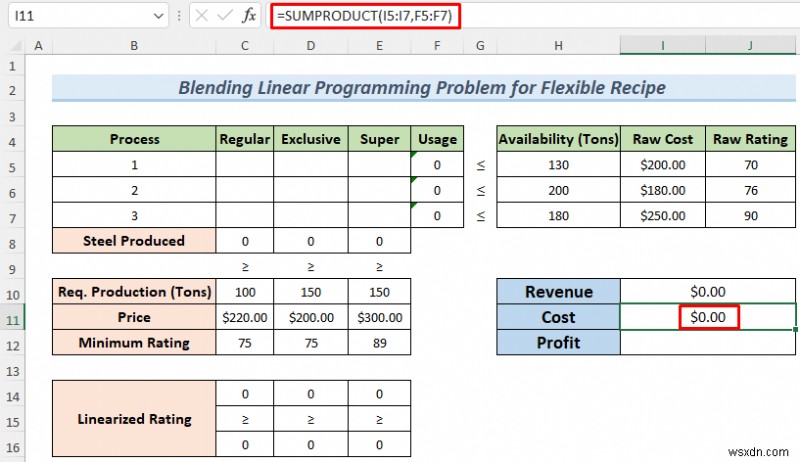
- And the following formula will return the Profit
=I10-I11
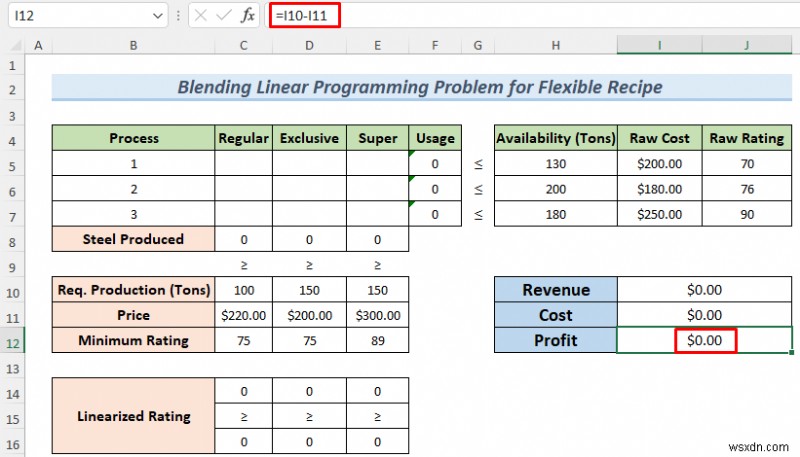
- After that, to enter the Subject , Changing Variable and Constraints , please follow the link of Method 1 that will lead you to the process. I’ll simply explain these inequalities in the following description.
- We want to maximize the profit amount, so we reference the cell that contains profit (I12 ).
- Next, our changing variables are the Steel products, so this range will be C5:E7 where the amount of production will be stored.
- After that, we added some constraints. The Linearized Raw Rating will be greater than or equal to Linearized Minimum Required Rating , so the range C14:E14 will be greater or equal to C16:E16 .
- Thereafter, the production amount will be greater than the required amount. So the range C8:E8 will be greater than C10:E10 .
- And the usage of raw materials will be lower than the available raw materials. So the range F5:F7 will be greater than H5:H7 .
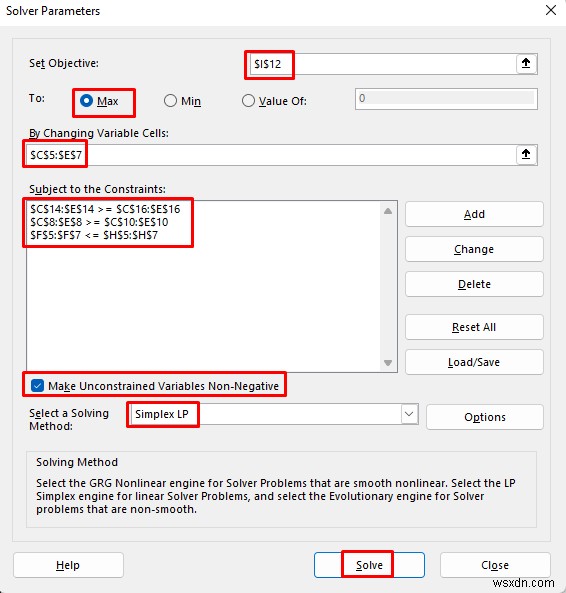
- After clicking on Solve , you will get the values of how much Raw Materials you should use to get the Maximum Profit .
- In addition, you will also get the results of Revenue , Chi phí of production and Profit .
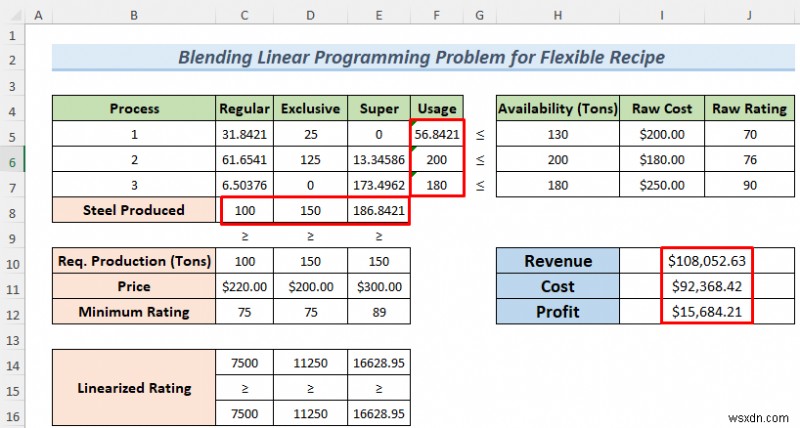
Thus you can solve the Blending Linear Programming problem with Excel Solver for the Flexible Recipe .
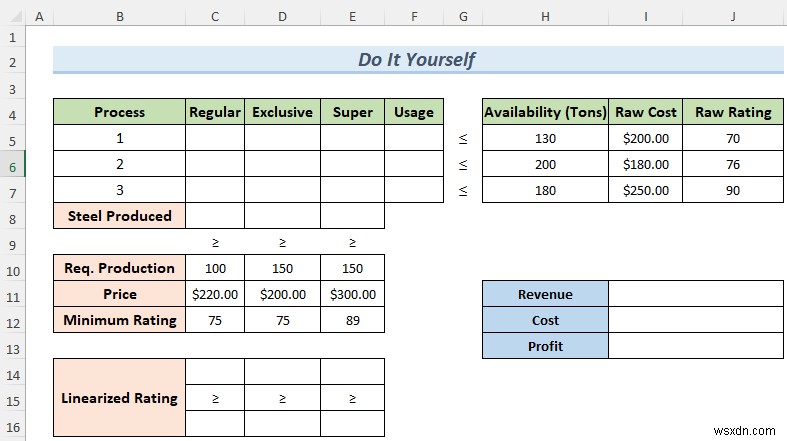
Phần thực hành
Here, I’m giving you the dataset of this article so that you can practice these methods on your own.
Kết luận
Suffice to say, you will achieve the basic idea of how to apply Blending Linear Programming to solve real life optimization problems with Excel Solver . If you have any better methods or questions or feedback regarding this article, please share them in the comment box. This will help me enrich my upcoming articles. For more queries, kindly visit our website ExcelDemy .
