Chương trình tìm hiểu xem BST có trong cây nhị phân nhất định bằng Python hay không

Giả sử chúng ta được cung cấp một cây nhị phân. Chúng ta phải tìm ra cây con lớn nhất từ ​​cây đó là cây tìm kiếm nhị phân (BST). Chúng tôi trả về nút gốc của BST.

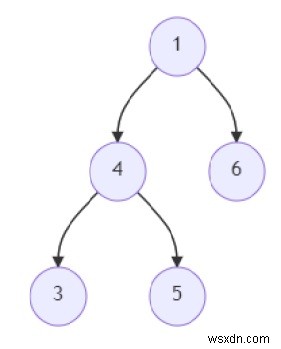
Vì vậy, nếu đầu vào giống như

thì đầu ra sẽ là -

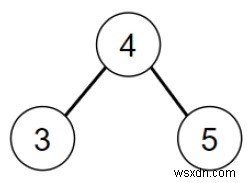
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• c:=0
• m:=null
• Định nghĩa một hàm recurse (). Điều này sẽ lấy nút
  • nếu nút không rỗng, thì
    • left_val:=recurse (bên trái của nút)
    • right_val:=recurse (bên phải của nút)
    • count:=âm vô cực
    • nếu (node.left giống với null hoặc node.left.val <=node.val) và (bên phải của node giống với null hoặc node.val <=node.right.val), thì
      • số lượng:=left_val + right_val + 1
    • nếu đếm> c, thì
      • c:=count
      • m:=nút
    • số lượng trả lại
  • trả về 0
• đệ quy (root)
• trả lại m

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

class TreeNode:
   def __init__(self, val, left = None, right = None):
      self.val = val
      self.left = left
      self.right = right

def insert(temp,data):
   que = []
   que.append(temp)
   while (len(que)):
      temp = que[0]
      que.pop(0)
      if (not temp.left):
         if data is not None:
            temp.left = TreeNode(data)
         else:
            temp.left = TreeNode(0)
         break
      else:
         que.append(temp.left)

      if (not temp.right):
         if data is not None:
            temp.right = TreeNode(data)
         else:
            temp.right = TreeNode(0)
         break
      else:
         que.append(temp.right)
def make_tree(elements):
   Tree= TreeNode(elements[0])
   for element in elements[1:]:
      insert(Tree, element)
   return Tree

def print_tree(root):
   if root is not None:
      print_tree(root.left)
      print(root.val, end = ', ')
      print_tree(root.right)

def solve(root):
   c, m = 0, None

   def recurse(node):
      if node:
         nonlocal c, m
         left_val = recurse(node.left)
         right_val = recurse(node.right)
         count = -float("inf")
         if (node.left == None or node.left.val <= node.val) and (node.right == None or node.val <= node.right.val):
            count = left_val + right_val + 1
         if count > c:
            c = count
            m = node
         return count
      return 0

   recurse(root)
   return m

tree = make_tree([1, 4, 6, 3, 5])
print_tree(solve(tree))

Đầu vào

tree = make_tree([1, 4, 6, 3, 5])
print_tree(solve(tree))

Đầu ra

3, 4, 5,