Giả sử chúng ta có một loại đồ thị đặc biệt có hai loại đỉnh được đặt tên là đầu và chân. Biểu đồ chỉ có một đầu và có k cạnh nối đầu với mỗi chân. Vì vậy, nếu chúng ta được cung cấp một đồ thị vô hướng, không có trọng số; chúng ta sẽ phải tìm ra những dạng đồ thị đặc biệt này trong đồ thị con rời rạc đỉnh của đồ thị. Hai đồ thị bất kỳ được coi là đỉnh rời rạc nếu chúng không có đỉnh chung.
Vì vậy, nếu đầu vào giống như
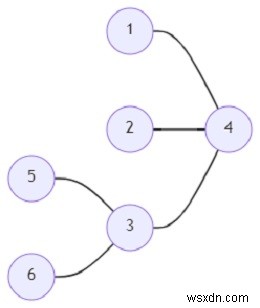
số nút (n) =5, số chân (t) =2, thì đầu ra sẽ là 5.
Có thể có 5 đồ thị đặc biệt như vậy là đồ thị con rời rạc đỉnh của đồ thị đã cho.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- G:=một danh sách mới chứa n + 1 danh sách trống
- đối với mỗi mục trong các cạnh, thực hiện
- s:=item [0]
- d:=item [1]
- chèn d vào cuối G [s]
- chèn s vào cuối G [d]
- thăm:=một bản đồ mới
- đối với tôi trong phạm vi từ 0 đến n, thực hiện
- v:=G [i]
- nếu kích thước của v bằng 1, thì
- s:=v [0]
- nếu không có mặt trong lượt truy cập, thì
- ghé thăm [s]:=[i]
- nếu không,
- thêm tôi vào cuối chuyến thăm [s]
- ngược lại khi kích thước của v bằng 0, thì
- n:=n - 1
- tmp:=0
- đối với mỗi k lượt truy cập, hãy thực hiện
- x:=kích thước lượt truy cập [k] -t
- nếu x> 0, thì
- tmp:=tmp + x
- return n - tmp
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
def solve(n, t, edges):
G = [[] for _ in range(n + 1)]
for item in edges:
s, d = map(int, item)
G[s].append(d)
G[d].append(s)
visit = {}
for i in range(n):
v = G[i]
if len(v) == 1:
s = v[0]
if s not in visit:
visit[s] = [i]
else: visit[s].append(i)
elif len(v) == 0:
n -= 1
tmp = 0
for k in visit:
x = len(visit[k])-t
if x > 0:
tmp += x
return n - tmp
print(solve(6, 2, [(1,4), (2,4), (3,4), (3,4), (5,3), (6,3)]))
Đầu vào
6, 2, [(1,4), (2,4), (3,4), (3,4), (5,3), (6,3)]
Đầu ra
5
