Giả sử chúng ta được cung cấp một đồ thị và được yêu cầu tìm ra kích thước nhỏ nhất của clique lớn nhất trong đồ thị. Một nhóm của đồ thị là một tập hợp con của đồ thị trong đó mọi cặp đỉnh đều kề nhau, tức là tồn tại một cạnh giữa mọi cặp đỉnh. Không thể tìm được nhóm lớn nhất trong một biểu đồ trong thời gian đa thức, vì vậy với số lượng nút và số cạnh của một biểu đồ nhỏ, chúng ta sẽ phải tìm ra nhóm lớn nhất trong đó.
Vì vậy, nếu đầu vào giống như các nút =4, các cạnh =4; thì đầu ra sẽ là 2.
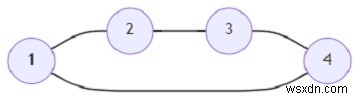
Trong biểu đồ trên, kích thước tối đa của một nhóm là 2.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- Xác định một hàm trợ giúp (). Điều này sẽ lấy x, y
- ga:=x mod y
- gb:=y - ga
- sa:=thương số của giá trị (x / y) + 1
- sb:=thương số của giá trị (x / y)
- return ga * gb * sa * sb + ga * (ga - 1) * sa * sa / 2 + gb * (gb - 1) * sb * sb / 2
- i:=1
- j:=node + 1
- while i + 1
- p:=i + giá trị sàn của ((j - i) / 2)
- k:=helper (các nút, p)
- nếu k
- i:=p
- j:=p
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
import math def helper(x, y): ga = x % y gb = y - ga sa = x // y + 1 sb = x // y return ga * gb * sa * sb + ga * (ga - 1) * sa * sa // 2 + gb * (gb - 1) * sb * sb // 2 def solve(nodes, edges): i = 1 j = nodes + 1 while i + 1 < j: p = i + (j - i) // 2 k = helper(nodes, p) if k < edges: i = p else: j = p return j print(solve(4, 4))
Đầu vào
4,4
Đầu ra
2
