Chương trình tìm giá trị màu lớn nhất trong biểu đồ có hướng bằng Python

Giả sử chúng ta có một đồ thị có hướng với n nút màu và m cạnh khác nhau. Và các nút được đánh số từ 0 đến n-1. Chúng ta có một chuỗi col với các chữ cái viết thường, trong đó col [i] đại diện cho màu của nút thứ i trong biểu đồ này (được lập chỉ mục 0). Chúng ta cũng có một danh sách cạnh mà các cạnh [j] =(u, v) biểu thị, có một cạnh giữa u và v.

Đường đi hợp lệ trong đồ thị là một chuỗi các nút xi với mọi i từ 1 đến k, sao cho có một cạnh hướng từ xi đến xi + 1. Màu của đường dẫn là màu nút thường xuyên nhất của đường dẫn đó. Chúng ta phải tìm giá trị màu lớn nhất của bất kỳ đường dẫn hợp lệ nào trong biểu đồ đó. Nếu có một chu kỳ trong đồ thị thì trả về -1.

Vì vậy, nếu đầu vào giống như col ="aabada" thì các cạnh =[(0,1), (1,4), (1,2), (2,3), (3,5), (4,5) ],

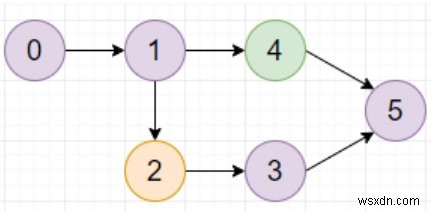
thì đầu ra sẽ là 4 vì 0 -> 1 -> 2 -> 3 -> 5 có đường dẫn dài nhất với màu 'a'.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

n:=kích thước của col
graph:=đồ thị đã cho từ danh sách cạnh
indgree:=bản đồ chứa các nút và giá trị trong độ của chúng
queue:=một danh sách mới
dp:=tạo một mảng có kích thước n x 26 và điền bằng 0
colorvalues:=tạo một danh sách với thứ tự c trong bảng chữ cái cho tất cả c trong col
đối với bạn trong phạm vi từ 0 đến n - 1, hãy thực hiện
- nếu bạn không mắc nợ, thì
  - chèn u vào cuối hàng đợi
  - dp [u, colorvalues [u]]:=1
đã truy cập:=0
trong khi hàng đợi không trống, thực hiện
- u:=phần tử trước của hàng đợi và xóa nó sau
- đã thăm:=đã thăm + 1
- đối với mỗi v trong biểu đồ [u], thực hiện
  - đối với c trong phạm vi từ 0 đến 25, thực hiện
    - dp [v, c] =tối đa của dp [v, c] và (dp [u, c] + (1 nếu c giống với giá trị màu [v], nếu không thì 0)
  - indgree [v]:=indgree [v] - 1
  - nếu indgree [v] giống 0 thì
    - chèn v vào cuối hàng đợi
    - del indgree [v]
nếu đã ghé thăm
- trả về -1
trả về phần tử tối đa trong dp

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau đây để hiểu rõ hơn

from collections import defaultdict
def solve(col, edges):
   n=len(col)
   graph=defaultdict(list)
   indegree=defaultdict(int)

   for u,v in edges:
      graph[u].append(v)
      indegree[v]+=1

   queue=[]
   dp=[[0]*26 for _ in range(n)]
   colorvalues=[ord(c)-ord("a") for c in col]
   for u in range(n):
      if u not in indegree:
         queue.append(u)
         dp[u][colorvalues[u]]=1

   visited=0
   while queue:
      u=queue.pop()
      visited+=1

      for v in graph[u]:
         for c in range(26):
            dp[v][c]=max(dp[v][c],dp[u][c] + (c==colorvalues[v]))
         indegree[v]-=1
         if indegree[v]==0:
            queue.append(v)
            del indegree[v]
   if visited<n:
      return -1
   return max(max(x) for x in dp)

col = "aabada"
edges = [(0,1),(1,4),(1,2),(2,3),(3,5),(4,5)]
print(solve(col, edges))

Đầu vào

"aabada", [(0,1),(1,4),(1,2),(2,3),(3,5),(4,5)]

Chương trình tìm giá trị màu lớn nhất trong biểu đồ có hướng bằng Python

Ví dụ

Đầu vào

Đầu ra