Giả sử có một đồ thị có trọng số với n đỉnh và m cạnh. Các cạnh có trọng số theo lũy thừa là 2. Có thể đạt được bất kỳ đỉnh nào từ bất kỳ đỉnh nào trong đồ thị và chi phí di chuyển sẽ là phép cộng của tất cả các trọng số cạnh trong đồ thị. Chúng ta sẽ phải xác định tổng chi phí tối thiểu giữa mỗi cặp đỉnh.
Vì vậy, nếu đầu vào giống như
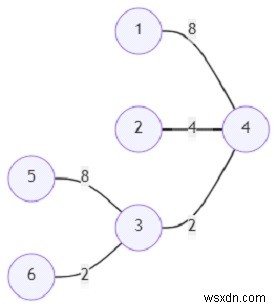
và số đỉnh (n) =6; thì đầu ra sẽ là 2696.
Tổng tất cả các khoảng cách là 2696.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- Định nghĩa một hàm par_finder (). Điều này sẽ đưa tôi, par
- nếu par [i] giống -1, thì
- trả lại tôi
- res:=par_finder (par [i], par)
- par [i]:=res
- trả lại res
- nếu par [i] giống -1, thì
- Xác định một hàm trợ giúp (). Điều này sẽ lấy i, par, w, G, n
- con:=1
- đối với mỗi mục trong G [i], thực hiện
- nếu mục [0] giống mệnh giá, thì
- chuyển sang lần lặp tiếp theo
- nếu không,
- child:=child + helper (item [0], i, item [1], G, n)
- nếu par không giống -1, thì
- ans:=ans + child * (n - child) * (1 * 2 ^ w)
- trả lại con
- nếu mục [0] giống mệnh giá, thì
- G:=một danh sách mới chứa n + 1 danh sách khác
- edge:=một danh sách mới
- đối với mỗi mục trên các con đường, hãy thực hiện
- u:=item [0]
- v:=item [1]
- w:=item [2]
- chèn (u-1, v-1, w) vào cuối các cạnh
- sắp xếp các cạnh danh sách theo trọng số của các cạnh
- par:=một danh sách mới có kích thước n + 1 được khởi tạo bằng -1
- r_edge:=một danh sách mới
- đối với mỗi i trong các cạnh, thực hiện
- nếu par_finder (i [0], par) giống par_finder (i [1], par), thì
- chuyển sang lần lặp tiếp theo
- nếu không,
- chèn i vào cuối r_edge
- chèn cặp (i [1], i [2]) vào cuối G [i [0]]
- chèn cặp (i [0], i [2]) vào cuối G [i [1]]
- par [par_finder (i [0], par)]:=par_finder (i [1], par)
- nếu par_finder (i [0], par) giống par_finder (i [1], par), thì
- ans:=0
- người trợ giúp (0, -1, 0, G, n)
- trả lại ans
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
def par_finder(i, par) : if par[i] == -1 : return i res = par_finder(par[i], par) par[i] = res return res def helper(i, par, w, G, n) : global ans child = 1 for item in G[i] : if item[0] == par : continue else : child += helper(item[0],i,item[1], G, n) if par != -1 : ans += child * (n - child) * (1 << w) return child def solve(n, roads): global ans G = [[] for i in range(n + 1)] edges = [] for item in roads : u,v,w = map(int, item) edges.append((u-1, v-1, w)) edges = sorted(edges,key = lambda item : item[2]) par = [-1 for i in range(n + 1)] r_edge = [] for i in edges : if par_finder(i[0], par) == par_finder(i[1], par) : continue else : r_edge.append(i) G[i[0]].append((i[1],i[2])) G[i[1]].append((i[0],i[2])) par[par_finder(i[0], par)] = par_finder(i[1], par) ans = 0 helper(0, -1, 0, G, n) return ans print(solve(6, [(1,4,8), (2,4,4), (3,4,4), (3,4,2), (5,3,8), (6,3,2)]))
Đầu vào
6, [(1,4,8), (2,4,4), (3,4,4), (3,4,2), (5,3,8), (6,3,2)]
Đầu ra
2696
