Chương trình để tìm ra đường dẫn chi phí tối thiểu giữa đỉnh có giá trị thấp nhất đến đỉnh có giá trị cao nhất (Python)

Giả sử chúng ta được cung cấp một đồ thị vô hướng, có trọng số và được yêu cầu tìm ra đường đi với chi phí đi lại tối thiểu có thể từ một nút cụ thể đến một nút cụ thể khác. Chi phí đi lại được tính như sau:giả sử có một con đường từ đỉnh A đến đỉnh C là A-> B-> C. Chi phí đi lại từ A đến B là 10 và chi phí đi từ B đến C là 20 .Chi phí đi từ A đến C sẽ là (chi phí đi từ A đến B) + (chênh lệch của chi phí đi lại từ B đến C và chi phí tích lũy của việc đi đến nút B). Vì vậy, điều đó sẽ dịch thành 10 + (20 - 10) =20. Chúng ta sẽ phải tìm ra các giá trị di chuyển tối thiểu có thể có trong nút đầu tiên đến nút cuối cùng (nút có giá trị thấp nhất đến nút có giá trị cao nhất) trong một biểu đồ nhất định.

Vì vậy, nếu đầu vào giống như

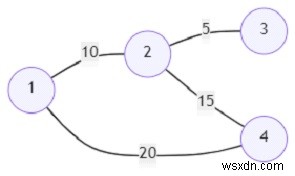
thì đầu ra sẽ là 15.

Tồn tại hai đường đi giữa các đỉnh 1 và 4. Đường đi tối ưu là 1-> 2-> 4, chi phí của đường đi là 10 + (15 - 10) =15. Nếu không, đường đi sẽ có giá 20.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• adjList:=một bản đồ mới chứa các danh sách trống
• đối với mỗi mục trong các cạnh, thực hiện
  • u:=item [0]
  • v:=item [1]
  • w:=item [2]
  • chèn cặp (w, v) vào cuối adjList [u]
  • chèn cặp (w, u) vào cuối adjList [v]
• q:=một heap mới
• v_list:=một tập hợp mới
• chèn (0,1) vào cuối q
• cờ:=True
• trong khi q không trống, hãy thực hiện
  • c:=bật mục nhỏ nhất từ ​​q
  • nếu c [1] có trong v_list, thì
    • chuyển sang lần lặp tiếp theo
  • thêm (c [1]) vào v_list
  • nếu c [1] giống với n, thì
    • cờ:=Sai
    • trả về c [0]
  • đối với mỗi u trong adjList [c [1]], thực hiện
    • nếu u [1] không có trong v_list, thì
      • out:=tối đa trong tổng số (u [0], c [0], u [1])
      • đẩy ra thành đống q
• nếu cờ là True thì
  • trả về -1

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

from collections import defaultdict
import heapq
def solve(n, edges):
    adjList = defaultdict(list)
    for item in edges:
        u, v, w = map(int, item)
        adjList[u].append((w,v))
        adjList[v].append((w,u))
    q = []
    v_list = set()
    q.append((0,1))
    flag = True
    while q:
        c = heapq.heappop(q)
        if c[1] in v_list:
            continue
        v_list.add(c[1])
        if c[1] == n:
            flag = False
            return c[0]
        for u in adjList[c[1]]:
            if u[1] not in v_list:
                out = (max(u[0],c[0]),u[1])
                heapq.heappush(q,out)    
    if flag:
        return -1

print(solve(4, [(1, 2, 10), (2, 3, 5), (2, 4, 15), (1, 4, 20)]))

Đầu vào

4, [(1, 2, 10), (2, 3, 5), (2, 4, 15), (1, 4, 20)]

Đầu ra

15