Chương trình tìm ra các cạnh quan trọng và giả quan trọng trong một biểu đồ bằng Python

Giả sử, chúng ta được cho một đồ thị chứa n đỉnh được đánh số từ 0 đến n -1. Đồ thị là vô hướng và mỗi cạnh có một trọng số. Vì vậy, với đồ thị, chúng ta phải tìm ra các cạnh tới hạn và giả tới hạn trong đồ thị MST. Một cạnh được gọi là cạnh tới hạn nếu việc xóa cạnh đó làm cho trọng số MST tăng lên. Một cạnh quan trọng giả là một cạnh có thể xuất hiện trong tất cả các MST của đồ thị, nhưng không phải tất cả. Chúng tôi tìm ra chỉ số của các cạnh cho biểu đồ làm đầu vào.

Vì vậy, nếu đầu vào giống như

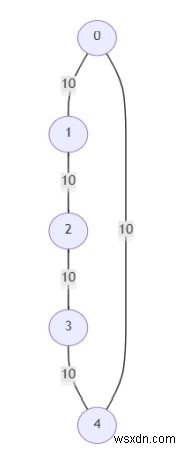
và số đỉnh là 5, thì đầu ra sẽ là [[], [0, 1, 2, 3, 4]] Không có cạnh tới hạn nào trong đồ thị đã cho và tất cả các cạnh đều là giả tới hạn. Vì tất cả các cạnh có cùng trọng số nên 3 cạnh bất kỳ từ biểu đồ sẽ tạo thành MST.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• Định nghĩa một hàm find_mst (). Điều này sẽ lấy num_vertices, graph, init:=null, exl:=null

• Xác định một hàm trợ giúp truy cập (). Điều này sẽ mất bạn

• k [u]:=Đúng

• đối với mỗi v, w trong biểu đồ [u, một danh sách trống], thực hiện

  • nếu exl và u ở exl và v ở exl, thì

    • chuyển sang lần lặp tiếp theo

  • nếu không k [v] là True thì

    • đẩy bộ ba (w, u, v) vào heap tmp

• res:=0

• k:=danh sách kích thước num_arrays mới chứa giá trị Sai

• tmp:=a new heap

• nếu init không phải là null thì

  • u:=init

  • v:=init

  • w:=init

  • res:=res + w

  • k [u]:=Đúng

  • k [v]:=Đúng

  • thăm (u) hoặc truy cập (v)

• nếu không,

  • ghé thăm (0)

• trong khi tmp không trống, thực hiện

  • w:=pop mục nhỏ nhất từ ​​heap tmp

  • u:=pop item nhỏ nhất từ ​​heap tmp

  • v:=pop mục nhỏ nhất từ ​​heap tmp

  • nếu k [u] và k [v] khác 0 thì

    • chuyển sang lần lặp tiếp theo

  • res:=res + w

  • nếu không k [u] là True thì

    • ghé thăm (u)

  • nếu không k [v] là True thì

    • thăm (v)

• trả về res nếu tất cả k là True, nếu không thì trả về vô cùng

• Từ phương thức chính, thực hiện như sau:

• graph:=đồ thị đã cho

• temp:=find_mst (num_vertices, graph)

• c_edge:=một danh sách mới

• p_edge:=một danh sách mới

• đối với tôi trong phạm vi từ 0 đến kích thước của các cạnh, hãy thực hiện

  • if find_mst (num_vertices, graph, exl =edge [i, index 2 to end])> temp, then

    • chèn tôi vào cuối c_edge

  • ngược lại, nếu find_mst (num_vertices, graph, init =edge [i]) giống với temp thì

    • chèn tôi vào cuối p_edge

• trả về [c_edge, p_edge]

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau đây để hiểu rõ hơn

from heapq import heappop, heappush
def solve(num_vertices, edges):
   graph = dict()
   for u, v, w in edges:
      graph.setdefault(u, []).append((v, w))
      graph.setdefault(v, []).append((u, w))
   temp = find_mst(num_vertices, graph)
   c_edge, p_edge = [], []
   for i in range(len(edges)):
      if find_mst(num_vertices, graph, exl = edges[i][:2]) > temp:
         c_edge.append(i)
      elif find_mst(num_vertices, graph, init = edges[i]) == temp:
         p_edge.append(i)
   return [c_edge, p_edge]


def find_mst(num_vertices, graph, init = None, exl = None):
   def visit(u):
      k[u] = True
      for v, w in graph.get(u, []):
         if exl and u in exl and v in exl:
            continue
         if not k[v]:
            heappush(tmp, (w, u, v))
   res = 0
   k = [False] * num_vertices
   tmp = []
   if init:
      u, v, w = init
      res += w
      k[u] = k[v] = True
      visit(u) or visit(v)
   else:
      visit(0)

   while tmp:
      w, u, v = heappop(tmp)
      if k[u] and k[v]: continue
      res += w
      if not k[u]:
         visit(u)
      if not k[v]:
         visit(v)
 
   return res if all(k) else inf

print(solve(5, [[0,1,10],[1,2,10],[2,3,10],[3,4,10],[4,0,10]]))

Đầu vào

5, [[0,1,10],[1,2,10],[2,3,10],[3,4,10],[4,0,10]]

Đầu ra

[[], [0, 1, 2, 3, 4]]