Giả sử chúng ta có một mảng được gọi là điểm với một số điểm ở dạng (x, y). Bây giờ chi phí nối hai điểm (xi, yi) và (xj, yj) là khoảng cách Manhattan giữa chúng, công thức là | xi - xj | + | yi - yj |. Chúng tôi phải tìm ra chi phí tối thiểu để kết nối tất cả các điểm.
Vì vậy, nếu đầu vào giống như điểm =[(0,0), (3,3), (2,10), (6,3), (8,0)], thì đầu ra sẽ là 22 vì
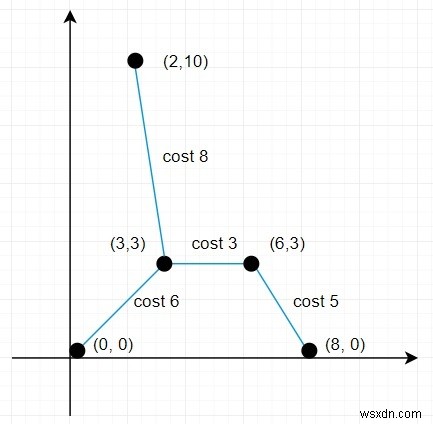
vì vậy tổng khoảng cách ở đây là (6 + 5 + 3 + 8) =22.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- points_set:=một tập hợp mới chứa các số từ phạm vi 0 đến kích thước của điểm - 1
- heap:=tạo một heap với cặp (0, 0)
- visit_node:=một tập hợp mới
- total_distance:=0
- trong khi heap không trống và kích thước của visit_node
- (distance, current_index):=xóa phần tử khỏi heap
- nếu current_index không có trong visit_node, thì
- chèn current_index vào visit_node
- xóa current_index khỏi points_set
- total_distance:=total_distance + khoảng cách
- (x0, y0):=điểm [current_index]
- đối với mỗi next_index trong points_set, hãy thực hiện
- (x1, y1):=điểm [next_index]
- insert (| x0 - x1 | + | y0 - y1 |, next_index) vào heap
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
import heapq def solve(points): points_set = set(range(len(points))) heap = [(0, 0)] visited_node = set() total_distance = 0 while heap and len(visited_node) < len(points): distance, current_index = heapq.heappop(heap) if current_index not in visited_node: visited_node.add(current_index) points_set.discard(current_index) total_distance += distance x0, y0 = points[current_index] for next_index in points_set: x1, y1 = points[next_index] heapq.heappush(heap, (abs(x0 - x1) + abs(y0 - y1), next_index)) return total_distance points = [(0,0),(3,3),(2,10),(6,3),(8,0)] print(solve(points))
Đầu vào
[(0,0),(3,3),(2,10),(6,3),(8,0)]
Đầu ra
22
