Giả sử chúng ta có một danh sách các danh sách được gọi là các cổng, trong đó các cổng [i] đại diện cho danh sách các cổng mà cổng i được kết nối. Chúng tôi cũng có một danh sách các danh sách khác được gọi là các lô hàng trong đó mỗi danh sách của dãy [i, j] biểu thị có một yêu cầu gửi hàng từ cảng i đến cảng j. Và chi phí để vận chuyển từ cảng i đến cảng j là chiều dài của con đường ngắn nhất từ hai cảng, chúng ta phải tìm tổng chi phí cần thiết để hoàn thành tất cả các chuyến hàng.
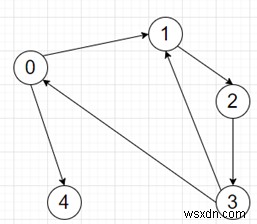
Vì vậy, nếu đầu vào giống như các cổng =[[1, 4], [2], [3], [0, 1], []] lô hàng =[[1, 4]], thì đầu ra sẽ là 4, vì đường dẫn là từ 1 -> 2 -> 3 -> 0 -> 4.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- n:=kích thước của các cổng
- dist:=ma trận kề từ danh sách các cổng
- đối với j trong phạm vi từ 0 đến n, thực hiện
- đối với tôi trong phạm vi từ 0 đến n, thực hiện
- đối với k trong phạm vi từ 0 đến n, thực hiện
- dist [i, k] =tối thiểu của dist [i, k], dist [i, j] + dist [j, k]
- đối với k trong phạm vi từ 0 đến n, thực hiện
- đối với tôi trong phạm vi từ 0 đến n, thực hiện
- đối với tất cả các lô hàng ở dạng [i, j], hãy lập danh sách dist [i, j] khi dist [i, j] không phải là vô cực
- trả về tổng danh sách đã tạo.
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn:
Ví dụ
class Solution: def solve(self, ports, shipments): n = len(ports) INF = 10 ** 10 dist = [[INF for _ in range(n)] for _ in range(n)] for i in range(n): dist[i][i] = 0 for i in range(n): for j in ports[i]: dist[i][j] = 1 for j in range(n): for i in range(n): for k in range(n): dist[i][k] = min(dist[i][k], dist[i][j] + dist[j][k]) return sum(dist[i][j] for i, j in shipments if dist[i][j] != INF) ob = Solution() ports = [[1, 4],[2],[3],[0, 1],[]] shipments = [[1, 4]] print(ob.solve(ports, shipments))
Đầu vào
[[1, 4],[2],[3],[0, 1],[]], [[1, 4]]
Đầu ra
4
