Trong bài viết này, chúng ta sẽ tìm hiểu về giải pháp cho câu hỏi được đưa ra bên dưới.
Tuyên bố sự cố - Chúng ta được đưa ra một ma trận chi phí và một vị trí (m, n), chúng ta cần tìm chi phí của đường chi phí tối thiểu để đạt (m, n) từ (0, 0). Mỗi ô biểu thị một chi phí để chuyển từ ô này sang ô khác.
Bây giờ chúng ta hãy quan sát giải pháp trong việc triển khai bên dưới -
Ví dụ
# dynamic approach
R = 3
C = 3
def minCost(cost, m, n):
# initialization
tc = [[0 for x in range(C)] for x in range(R)]
# base case
tc[0][0] = cost[0][0]
# total cost(tc) array
for i in range(1, m + 1):
tc[i][0] = tc[i-1][0] + cost[i][0]
# tc array
for j in range(1, n + 1):
tc[0][j] = tc[0][j-1] + cost[0][j]
# rest tc array
for i in range(1, m + 1):
for j in range(1, n + 1):
tc[i][j] = min(tc[i-1][j-1], tc[i-1][j], tc[i][j-1]) + cost[i][j]
return tc[m][n]
# main
cost = [[1, 5, 3],
[7, 7, 4],
[8, 5, 3]]
print("Total Cost:",minCost(cost, 2, 1)) Đầu ra
Total Cost: 13
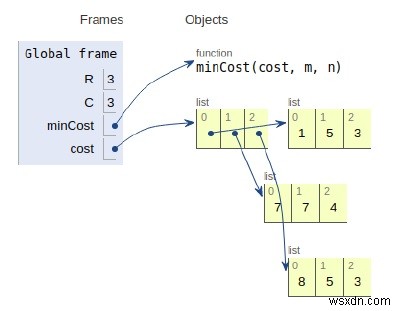
Tất cả các biến được khai báo trong phạm vi cục bộ và các tham chiếu của chúng được hiển thị trong hình trên.
Kết luận
Trong bài viết này, chúng ta đã tìm hiểu về cách tạo Chương trình Python cho Đường dẫn Chi phí Tối thiểu
