Luôn luôn có hai nghiệm thức thực của một số dương. Ví dụ, nếu x2 là 25, x là ± 5. Tuy nhiên, nếu x2 là -25 gốc thực thì không tồn tại. Căn bậc hai của bất kỳ số âm nào là căn bậc hai của giá trị tuyệt đối của nó nhân với một đơn vị ảo j =√ − 1.
Do đó √ − 25 =√25 𝑋 − 1 =√25 × √ − 1 =5j
Một số phức bao gồm thành phần thực và ảo. Nó được biểu diễn dưới dạng x + yj. Cả x và y đều là số thực. Y nhân với đơn vị ảo sẽ tạo thành một phần ảo của số phức.
Ví dụ:3 + 2j, 10-5.5J, 9.55 + 2.3j, 5.11e-6 + 4j
Python có một kiểu dữ liệu phức hợp được tích hợp sẵn. Một đối tượng số phức có thể được tạo bằng cách biểu diễn theo nghĩa đen như sau -
>>> x = 2+3j >>> type(x)
Đối tượng số phức có hai thuộc tính real (trả về thành phần thực) và hình ảnh (trả về thành phần ảo không bao gồm đơn vị ảo j)
>>> x.real 2.0 >>> x.imag 3.0
Nó cũng có liên từ () phương pháp. Hợp của một số phức có cùng thành phần thực và thành phần ảo cùng dấu. Do đó liên hợp của 2 + 3j là 2-3j
>>> x.conjugate() (2-3j)
Python cũng có sẵn hàm complex () trả về một đối tượng số phức. Hàm nhận hai tham số, mỗi tham số cho thành phần thực và ảo. Chúng có thể thuộc bất kỳ kiểu số nào (int, float hoặc complex)
>>> complex(9,5) (9+5j) >>> complex(-6, -2.5) (-6-2.5j) >>> complex(1.5j, 2.5j) (-2.5+1.5j)
Nếu chỉ có một tham số được cung cấp, nó được coi là thành phần thực, thành phần ảo được coi là bằng không.
>>> complex(15) (15+0j)
Hàm cũng có thể nhận một chuỗi làm đối số miễn là nó chứa biểu diễn số.
>>> complex('51')
(51+0j)
>>> complex('1.5')
(1.5+0j) Phép cộng và phép trừ số phức cũng tương tự như phép cộng và phép trừ số nguyên. Các phần thực và ảo được thêm / bớt riêng biệt.
>>> a = 6+4j >>> b = 3+6j >>> a+b (9+10j) >>> a-b (3-2j)
Đối với phép nhân, hãy coi số phức là một nhị thức và nhân mỗi số hạng ở số thứ nhất với mỗi số hạng ở số thứ hai.
a = 6+4j b = 3+2j c = a*b c = (6+4j)*(3+2j) c = (18+12j+12j+8*-1) c = 10+24j
Trong bảng điều khiển Python, kết quả xác minh điều này -
>>> a = 6+4j >>> b = 3+2j >>> a*b (10+24j)
Phép chia các số phức được thực hiện như sau -
Giả sử hai số là
a =2 + 4j
b =1-2j
và chúng tôi muốn tính a / b.
Lấy liên hợp của mẫu số là 1 + 2j
Nhân tử số và mẫu số với liên từ của mẫu số để nhận kết quả của phép chia
c = a/b c = (2+4j)*(1+2j)/(1-2j)(1+2j) c = (2+4j+4j+8*-1)/(1+2j-2j-4*-1) c = (-6+8j)/5 c = -1.2+1.6j
Sau phiên bảng điều khiển Python xác minh cách xử lý ở trên.
>>> a = 2+4j >>> b = 1-2j >>> a/b (-1.2+1.6j)
Mô-đun cmath
Các hàm toán học được xác định trong mô-đun toán học của thư viện tiêu chuẩn của Python xử lý số dấu phẩy động. Đối với số phức, thư viện Python chứa mô-đun cmath.
Số phức z =x + yj là một biểu diễn Descartes. Nó được biểu diễn bên trong bằng tọa độ cực với môđun của nó là r (được trả về bởi hàm abs () tích hợp sẵn) và góc pha Φ (phát âm là phi) là góc ngược chiều kim đồng hồ tính bằng radian, giữa trục x và đường nối x với nguồn gốc. Sơ đồ sau minh họa biểu diễn cực của số phức -
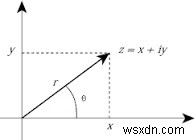
Các hàm trong mô-đun cmath cho phép chuyển đổi biểu diễn Descartes sang biểu diễn cực và ngược lại.
polar () - Hàm này trả về biểu diễn cực của ký hiệu Descartes của số phức. Giá trị trả về là một bộ bao gồm mô đun và pha.
>>> import cmath >>> a = 2+4j >>> cmath.polar(a) (4.47213595499958, 1.1071487177940904)
Lưu ý rằng mô-đun được trả về bởi hàm abs ()
>>> abs(a) 4.47213595499958
phase () - Hàm này trả về góc ngược chiều kim đồng hồ giữa trục x và đoạn nối a với nguồn gốc. Góc được biểu thị bằng radian và nằm trong khoảng từ π đến -π
>>> cmath.phase(a) 1.1071487177940904 z = x+yj Φ
direct () - Hàm này trả về biểu diễn Descartes của số phức được biểu diễn ở dạng cực, tức là trong mô đun và pha
>>> cmath.rect(4.47213595499958, 1.1071487177940904) (2.0000000000000004+4j)
Mô-đun cmath chứa các lựa chọn thay thế cho tất cả các hàm toán học được xác định trong mô-đun toán học. Có các hàm lượng giác và logarit như được giải thích bên dưới -
cmath.sin () - Hàm này trả về tỷ số lượng giác sin cho góc pha được biểu thị bằng radian.
>>> import cmath >>> a = 2+4j >>> p = cmath.phase(a) >>> cmath.sin(p) (0.8944271909999159+0j)
Tương tự, các hàm cho các tỷ lệ khác cos (), tan (), asin (), acos () và atan () được định nghĩa trong mô-đun cmath.
cmath.exp () - Tương tự như math.exp (), hàm này trả về ex trong đó x là số phức và e là 2.71828
>>> cmath.exp(a) (-1.1312043837568135+2.4717266720048188j)
cmath.log10 () - Hàm này tính toán giá trị log của số phức lấy cơ số là 10
>>> a = 1+2j >>> cmath.log10(a) (0.3494850021680094+0.480828578784234j)
cmath.sqrt () - Hàm này trả về căn bậc hai của số phức.
>>> cmath.sqrt(a) (1.272019649514069+0.7861513777574233j)
Trong bài viết này, chúng ta đã tìm hiểu các tính năng quan trọng của kiểu dữ liệu số phức của Python và cách các phép toán số học có thể được thực hiện trên nó. Chúng tôi cũng đã khám phá các chức năng khác nhau được định nghĩa trong mô-đun cmath.
