Bất kỳ số nào có thể biểu diễn dưới dạng thương số hoặc phân số dưới dạng p / q đều được gọi là số hữu tỉ. Mô-đun phân số của thư viện Python cung cấp chức năng cho số học hữu tỉ.
Mô-đun này định nghĩa một lớp Phân số. Đối tượng của nó có thể được cấu thành theo nhiều cách khác nhau như sau -
Fraction(num, denom)
Phiên bản đầu tiên của hàm tạo phân số nhận hai tham số cho tử số và mẫu số. Tử số mặc định là 0 và mẫu số mặc định là 1. Giá trị của mẫu số =0 ném ZeroDivisionError.
>>> from fractions import Fraction >>> n1 = Fraction(2,5) >>> n1 Fraction(2, 5) >>> n2 = Fraction(6,15) >>> n2 Fraction(2, 5) >>> n3 = Fraction(10,1) >>> n3 Fraction(10, 1) >>> n3 = Fraction(10) >>> n3 Fraction(10, 1)
Lưu ý rằng các tham số tử số và mẫu số được giảm xuống các giá trị nhỏ nhất sau khi chia chúng cho các thừa số chung.
Hàm tạo phân số cũng có thể nhận tham số chuỗi miễn là nó chứa biểu diễn số hợp lệ.
>>> n1 = Fraction('5')
>>> n1
Fraction(5, 1)
>>> n2 = Fraction('4/7')
>>> n2
Fraction(4, 7)
>>> n3 = Fraction('0.25')
>>> n3
Fraction(1, 4)
>>> n4 = Fraction('1.23E4')
>>> n4
Fraction(12300, 1) Một số dấu phẩy động cũng có thể là một tham số cho hàm tạo. Tuy nhiên, do biểu diễn float ở dạng nhị phân thuần túy, thương số của tử số và mẫu số của đối tượng Phân số kết quả có thể không chính xác. Mặt khác, một đối tượng của lớp Decimal làm tham số cũng tạo ra đối tượng Fraction.
>>> from fractions import Fraction
>>> from decimal import Decimal
>>> n1 = Fraction(2.1)
>>> n1
Fraction(4728779608739021, 2251799813685248)
>>> n2 = Fraction(Decimal('2.1'))
>>> n2
Fraction(21, 10) Tất cả các phép toán số học đều được phép với các đối tượng Phân số.
>>> n1 = Fraction(2,3) >>> n2 = Fraction(1,2) >>> n1+n2 Fraction(7, 6) >>> n1-n2 Fraction(1, 6) >>> n1*n2 Fraction(1, 3) >>> n1/n2 Fraction(4, 3)
Chỉ để nhớ lại cách số học ngẫu nhiên được thực hiện ở dạng thương số -
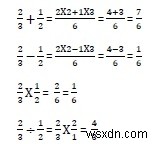
Đối tượng phân số có hai thuộc tính, tử số và mẫu số có thể được truy cập độc lập.
>>> n1 = Fraction(2,3) >>> n1.numerator 2 >>> n1.denominator 3
Lớp Phân số có các phương thức hữu ích sau để tìm số nguyên lớn nhất nhỏ hơn thương (giá trị sàn) và một số nguyên nhỏ nhất lớn hơn thương (giá trị ceil)
>>> n1 = Fraction(355,113) >>> n1.__floor__() 3 >>> n1.__ceil__() 4
Một phương thức lớp khác limit_denominator () trả về phân số gần nhất có mẫu số nhiều nhất bằng giá trị được chỉ định.
>>> Fraction('2.71828').limit_denominator(400)
Fraction(1071, 394) Trong bài viết này, các tính năng và chức năng trong mô-đun phân số của thư viện chuẩn Python đã được thảo luận.
