Giả sử chúng ta có một cây nhị phân; chúng ta phải tìm đường dẫn dài nhất trong cây nhị phân.
Vì vậy, nếu đầu vào giống như
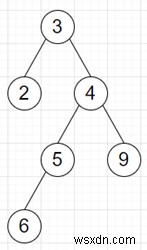
thì đầu ra sẽ là 5 vì chuỗi liên tiếp dài nhất là [2, 3, 4, 5, 6].
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- nếu gốc là null, thì
- trả về 0
- maxPath:=0
- Xác định một hàm trợ giúp (). Điều này sẽ lấy nút
- inc:=1, dec:=1
- nếu bên trái của nút không rỗng, thì
- [left_inc, left_dec]:=helper (bên trái của nút)
- nếu không,
- [left_inc, left_dec]:=[0, 0]
- nếu bên phải của nút không rỗng, thì
- [right_inc, right_dec]:=helper (bên phải của nút)
- nếu không,
- [right_inc, right_dec]:=[0, 0]
- nếu bên trái của nút không rỗng và giá trị của nút - giá trị bên trái của nút bằng 1, thì
- inc:=tối đa trong tổng số inc và (left_inc + 1)
- nếu không, khi bên trái của nút không rỗng và giá trị của nút - giá trị bên trái của nút giống -1, thì
- dec:=tối đa là dec và (left_dec + 1)
- nếu bên phải của nút không rỗng và giá trị của nút - giá trị của bên phải của nút bằng 1, thì
- inc:=tối đa trong tổng số inc và (right_inc + 1)
- ngược lại khi bên phải của nút không rỗng và giá trị của nút - giá trị của bên phải của nút bằng -1, thì
- dec:=tối đa là dec và (right_dec + 1)
- nếu bên trái của nút không phải là null và bên phải của nút không phải là null và giá trị của bên trái của nút - giá trị của nút bằng 1 và giá trị của nút - giá trị của bên phải của nút bằng 1, thì
- maxPath:=tối đa của maxPath và (left_dec + right_inc + 1)
- nếu không khi bên trái của nút không phải là null và bên phải của nút không phải là null và giá trị của bên trái của nút - giá trị của nút bằng -1, thì
- maxPath:=tối đa maxPath và (left_inc + right_dec + 1)
- maxPath:=tối đa của maxPath, inc và dec
- return inc, dec
- Từ phương thức chính, hãy làm như sau:
- người trợ giúp (gốc)
- trả về maxPath
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
Ví dụ
class TreeNode: def __init__(self, data, left = None, right = None): self.val = data self.left = left self.right = right def print_tree(root): if root is not None: print_tree(root.left) print(root.val, end = ', ') print_tree(root.right) class Solution: def solve(self, root): if not root: return 0 self.maxPath = 0 def helper(node): inc, dec = 1, 1 if node.left: left_inc, left_dec = helper(node.left) else: left_inc, left_dec = 0, 0 if node.right: right_inc, right_dec = helper(node.right) else: right_inc, right_dec = 0, 0 if node.left and node.val - node.left.val == 1: inc = max(inc, left_inc + 1) elif node.left and node.val - node.left.val == -1: dec = max(dec, left_dec + 1) if node.right and node.val - node.right.val == 1: inc = max(inc, right_inc + 1) elif node.right and node.val - node.right.val == -1: dec = max(dec, right_dec + 1) if (node.left and node.right and node.left.val - node.val == 1 and node.val - node.right.val == 1): self.maxPath = max(self.maxPath, left_dec + right_inc + 1) elif (node.left and node.right and node.left.val - node.val == -1 and node.val - node.right.val == -1): self.maxPath = max(self.maxPath, left_inc + right_dec + 1) self.maxPath = max(self.maxPath, inc, dec) return inc, dec helper(root) return self.maxPath ob = Solution() root = TreeNode(3) root.left = TreeNode(2) root.right = TreeNode(4) root.right.left = TreeNode(5) root.right.right = TreeNode(9) root.right.left.left = TreeNode(6) print(ob.solve(root))
Đầu vào
root = TreeNode(3) root.left = TreeNode(2) root.right = TreeNode(4) root.right.left = TreeNode(5) root.right.right = TreeNode(9) root.right.left.left = TreeNode(6)
Đầu ra
5
