Chương trình tìm độ dài của đường đi dài nhất trong cây n-ary bằng Python

Giả sử chúng ta có một danh sách cạnh trong đó mỗi mục đang giữ (u, v) đại diện cho u là cha của v. Chúng ta phải tìm độ dài của đường đi dài nhất trong cây. Độ dài đường dẫn là 1 + số nút trong đường dẫn đó.

Vì vậy, nếu đầu vào giống như

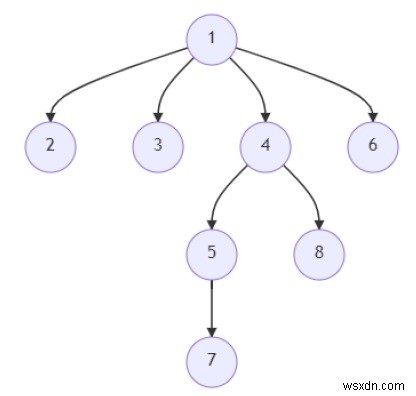
thì đầu ra sẽ là 5, vì đường dẫn là [1, 4, 5, 7], có tổng cộng 4 nút, do đó độ dài đường dẫn là 1 + 4 =5.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• g:=danh sách gần kề của biểu đồ từ danh sách cạnh đã cho
• d:=một bản đồ mới
• Định nghĩa một hàm bfs (). Điều này sẽ mất o
• d [o]:=1
• f:=o
• q:=[o]
• với mỗi x trong q, thực hiện
  • đối với mỗi y trong g [x], thực hiện
    • nếu y không nằm trong d, thì
      • d [y]:=d [x] + 1
      • nếu d [y]> d [f], thì
        • f:=y
      • chèn y vào q
• return f
• Từ phương pháp chính, hãy thực hiện như sau -
• đối với mỗi o trong g, thực hiện
  • f:=bfs (o)
  • d:=một bản đồ mới
  • return d [bfs (f)]
• trả về 0

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

def solve(edges):
   g = {}
   for u, v in edges:
      if u not in g:
         g[u] = []
      g[u] += (v,)
      if v not in g:
         g[v] = []
      g[v] += (u,)
   d = {}

   def bfs(o):
      d[o] = 1
      f = o
      q = [o]
      for x in q:
         for y in g[x]:
            if y not in d:
               d[y] = d[x] + 1
               if d[y] > d[f]:
                  f = y
               q += (y,)
      return f

   for o in g:
      f = bfs(o)
      d = {}
      return d[bfs(f)]
   return 0

edges = [(1, 2),(1, 3),(1, 4),(4, 5),(5,7),(1,6),(4,8)]
print(solve(edges))

Đầu vào

[(1, 2),(1, 3),(1, 4),(4, 5),(5,7),(1,6),(4,8)]

Đầu ra

5