Chương trình tìm ra tổ tiên chung thấp nhất của cây nhị phân bằng Python

Giả sử, chúng ta được cung cấp một cây nhị phân và hai nút cụ thể x và y. Chúng ta phải tìm ra tổ tiên chung thấp nhất của hai nút từ cây nhị phân. Tổ tiên chung thấp nhất trong cây nhị phân là nút thấp nhất mà cả hai nút x và y đều là con cháu của nó. Ngoài ra, một nút cụ thể cũng có thể là con của chính nó. Chúng tôi phải tìm nút và trả về nó dưới dạng đầu ra.

Vì vậy, nếu đầu vào giống như

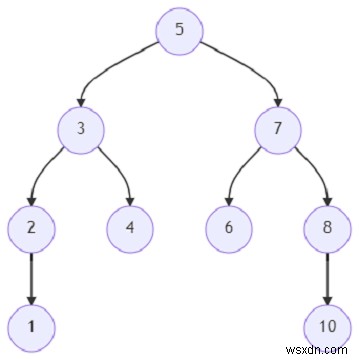
và x =2, y =4; thì đầu ra sẽ là 3.

Nút mà các nút 2 và 4 là con của nút 3. Vì vậy, 3 sẽ được trả về.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• Định nghĩa một hàm dfs (). Điều này sẽ lấy nút

  • nếu nút tương tự như null, thì

    • trở lại

  • nếu nút có trong danh sách [x, y] thì

    • left:=dfs (left of node)

    • right:=dfs (bên phải của nút)

    • nếu trái hoặc phải khác 0 thì

      • ans:=nút

      • nút trả lại

  • left:=dfs (left of node)

  • right:=dfs (bên phải của nút)

  • nếu trái và phải không rỗng thì

    • ans:=nút

    • nút trả lại

  • quay lại trái hoặc phải

• ans:=dfs (root)

• trả lại ans

Ví dụ

class TreeNode:
def __init__(self, data, left = None, right = None):
   self.data = data
   self.left = left
   self.right = right
def insert(temp,data):
   que = []
   que.append(temp)
   while (len(que)):
      temp = que[0]
      que.pop(0)
      if (not temp.left):
      if data is not None:
         temp.left = TreeNode(data)
      else:
         temp.left = TreeNode(0)
         break
      else:
         que.append(temp.left)
      if (not temp.right):
      if data is not None:
         temp.right = TreeNode(data)
      else:
         temp.right = TreeNode(0)
         break
      else:
         que.append(temp.right)
def make_tree(elements):
   Tree = TreeNode(elements[0])
   for element in elements[1:]:
      insert(Tree, element)
      return Tree
def search_node(root, element):
   if (root == None):
      return None
   if (root.data == element):
      return root
      res1 = search_node(root.left, element)
   if res1:
      return res1
      res2 = search_node(root.right, element)
      return res2
def solve(root, x, y):
def dfs(node):
   if not node:
      return
   if node in [x,y]:
      left = dfs(node.left)
      right = dfs(node.right)
   if left or right:
      ans = node
      return node
      left = dfs(node.left)
      right = dfs(node.right)
   if left and right:
      ans = node
      return node
      return left or right
      ans = dfs(root)
   return ans
root = make_tree([5, 3, 7, 2, 4, 1, 7, 6, 8, 10])
print(solve(root, search_node(root, 2), search_node(root, 4)).data)

Đầu vào

make_tree([5, 3, 7, 2, 4, 1, 7, 6, 8, 10]),
search_node(root, 2),
search_node(root, 4)

Đầu ra

3