Chương trình thêm hai đa thức đã cho dưới dạng danh sách liên kết bằng Python

Giả sử, chúng ta được cho hai đa thức và chúng ta phải tìm phép cộng của hai đa thức. Các đa thức phải được biểu diễn dưới dạng danh sách liên kết; các điều khoản của đa thức sẽ được biểu diễn dưới dạng một nút danh sách liên kết. Mỗi nút danh sách được liên kết sẽ chứa giá trị hệ số, giá trị lũy thừa và con trỏ đến nút danh sách liên kết tiếp theo. Chúng ta phải trả về một danh sách được liên kết thứ ba là sự bổ sung của hai đa thức danh sách được liên kết.

Vì vậy, nếu đầu vào giống như

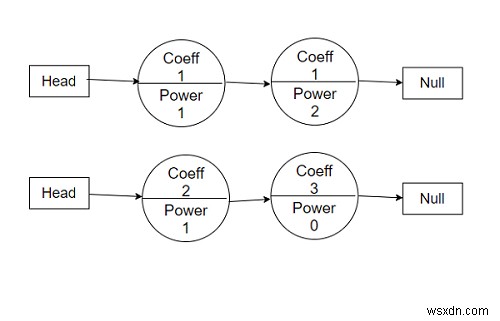
1x ^ 1 + 1x ^ 2 =0 và 2x ^ 1 + 3x ^ 0 =0,

thì đầu ra sẽ là 3x ^ 1 + 1x ^ 2 + 3x ^ 0 =0

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• dummy:=một nút đa thức mới

• node:=a new polynomial node

• trong khi poly1 và poly2 không trống, thực hiện

  • nếu sức mạnh của poly1> sức mạnh của poly2, thì

    • tiếp theo của nút:=poly1

    • nút:=poly1

    • poly1:=tiếp theo của poly1

  • ngược lại khi lũy thừa của poly1

    • tiếp theo của nút:=poly2

    • nút:=poly2

    • poly2:=tiếp theo của poly2

  • nếu không,

    • coef:=hệ số của poly1 + hệ số của poly2

    • nếu coef khác 0 thì

      • poly1:=tiếp theo của poly1

      • poly2:=tiếp theo của poly2

• tiếp theo của nút:=poly1 hoặc poly2

• trở lại tiếp theo của hình nộm

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

Ví dụ

class polynomial:
def __init__(self, coeff = 0, pow = 0, nxt = None):
   self.coefficient = coeff
   self.power = pow
   self.next = nxt
def create_poly(expression):
   head = None
   for element in expression:
      if head == None:
         head = polynomial(element[0], element[1])
      else:
         temp = head
      while temp.next != None:
         temp = temp.next
         if temp.next == None:
            temp.next = polynomial(element[0], element[1])
            return head
def show_poly(head):
   temp = head
   while temp.next != None:
      print(str(temp.coefficient) + 'x^' + str(temp.power), end = ' + ')
      temp = temp.next
      if temp.next == None:
         print(str(temp.coefficient) + 'x^' + str(temp.power), end=' = 0')
def solve(poly1, poly2):
   dummy = node = polynomial()
   while poly1 and poly2:
      if poly1.power > poly2.power:
         node.next = node = poly1
         poly1 = poly1.next
      elif poly1.power < poly2.power:
         node.next = node = poly2
         poly2 = poly2.next
      else:
         coef = poly1.coefficient + poly2.coefficient
      if coef: node.next = node = polynomial(coef, poly1.power)
         poly1 = poly1.next
         poly2 = poly2.next
         node.next = poly1 or poly2
   return dummy.next
poly1 = create_poly([[1,1], [1,2]])
poly2 = create_poly([[2,1], [3, 0]])
poly3 = solve(poly1, poly2)
show_poly(poly3)

Đầu vào

poly1 = create_poly([[1,1], [1,2]])
poly2 = create_poly([[2,1], [3, 0]])

Đầu ra

3x^1 + 1x^2 + 3x^0 = 0