Giả sử, chúng ta được đưa cho một cây n-ary và được cho là xác định đường kính của cây. Đường kính của cây là đường đi dài nhất giữa hai nút lá bất kỳ của cây. Chúng ta phải tìm ra và trả về giá trị nguyên đại diện cho đường kính của cây.
Vì vậy, nếu đầu vào giống như
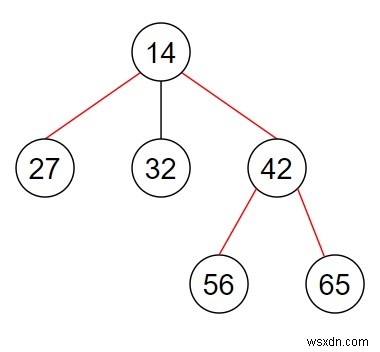
thì đầu ra sẽ là 3.
Đường kính của cây n-ary này bao gồm các cạnh 27-> 14, 14-> 42 và 42-> 56 hoặc 42-> 65 (được đánh dấu trong sơ đồ bằng các đường màu đỏ). Chiều dài đường dẫn là 3.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
-
ans:=1
-
Xác định độ sâu của hàm (). Điều này sẽ bắt nguồn từ gốc
-
nếu gốc không trống, thì
-
trả về 0
-
-
Children:=một danh sách mới chứa các giá trị 0, 0
-
temp_children:=một danh sách mới
-
đối với mỗi đứa trẻ trong phần con của gốc, hãy thực hiện
-
chèn độ sâu (con) vào cuối temp_children
-
-
nếu kích thước của (temp_children)> 0, thì
-
trẻ em:=temp_children
-
-
ans:=tối đa ans, sum (sắp xếp danh sách con [từ độ dài chỉ mục của (con) - 2 đến cuối]) + 1
-
trả lại tối đa con + 1
-
-
độ sâu (gốc)
-
return (ans -1)
Ví dụ (Python)
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
Nútclass Node: def __init__(self, value, child = None) -> None: self.val = value self.children = [] if child != None: for value in child: self.children.append(value) ans = 1 def solve(root): def depth(root): global ans if not root: return 0 children = [0, 0] temp_children = [depth(child) for child in root.children] if len(temp_children) > 0: children = temp_children ans = max(ans, sum(sorted(children)[-2:]) + 1) return max(children) + 1 depth(root) return ans -1 node6 = Node(65) node5 = Node(56) node4 = Node(42, [node5, node6]) node3 = Node(32) node2 = Node(27) node1 = Node(14, [node2, node3, node4]) root = node1 print(solve(root))
Đầu vào
node6 = Node(65) node5 = Node(56) node4 = Node(42, [node5, node6]) node3 = Node(32) node2 = Node(27) node1 = Node(14, [node2, node3, node4]) root = node1
Đầu ra
3
