Chương trình tìm đường dẫn độ dài k trên cây nhị phân bằng Python

Giả sử chúng ta có một cây nhị phân chứa các giá trị duy nhất và chúng ta cũng có một giá trị khác k, chúng ta phải tìm số đường đi duy nhất có độ dài k trong cây. Các đường dẫn có thể đi từ cha mẹ sang con hoặc từ con đến cha mẹ. Chúng tôi sẽ coi hai đường dẫn là khác nhau khi một số nút xuất hiện trong một đường dẫn nhưng không xuất hiện trong đường dẫn kia.

Vì vậy, nếu đầu vào giống như

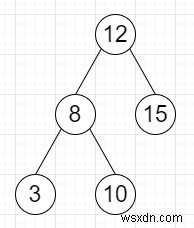
k =3, thì đầu ra sẽ là 4, vì các đường dẫn là [12,8,3], [12,8,10], [8,12,15], [3,8,10].

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau−

• Định nghĩa một hàm dfs (). Điều này sẽ lấy nút

  • nếu nút là null, thì

    • trả về danh sách có 1 và k-1 số 0

  • left:=dfs (left of node)

  • right:=dfs (bên phải của nút)

  • đối với tôi trong phạm vi từ 0 đến K, hãy thực hiện

    • ans:=ans + left [i] * right [K - 1 - i]

  • res:=danh sách kích thước K gồm 0s

  • res [0]:=1, res [1]:=1

  • đối với tôi trong phạm vi từ 1 đến K - 1, hãy thực hiện

    • res [i + 1]:=res [i + 1] + left [i]

    • res [i + 1]:=res [i + 1] + right [i]

  • trả lại res

• Từ phương thức chính, hãy thực hiện như sau−

• ans:=0

• 
  

• dfs (gốc)

• 
  

• trả lại ans

  
  

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

Ví dụ

class TreeNode:
   def __init__(self, data, left = None, right = None):
      self.data = data
      self.left = left
      self.right = right
class Solution:
   def solve(self, root, K):
      def dfs(node):
         if not node:
            return [1] + [0] * (K-1)
         left = dfs(node.left)
         right = dfs(node.right)
         for i in range(K):
            self.ans += left[i] * right[K - 1 - i]
         res = [0] * K
         res[0] = res[1] = 1
         for i in range(1, K - 1):
            res[i + 1] += left[i]
            res[i + 1] += right[i]
         return res
      self.ans = 0
      dfs(root)
      return self.ans
ob = Solution()
root = TreeNode(12)
root.left = TreeNode(8)
root.right = TreeNode(15)
root.left.left = TreeNode(3)
root.left.right = TreeNode(10)
print(ob.solve(root, 3))

Đầu vào

root = TreeNode(12)
root.left = TreeNode(8)
root.right = TreeNode(15)
root.left.left = TreeNode(3)
root.left.right = TreeNode(10)
3

Đầu ra

4