Một đồ thị xoay chiều có trọng số được đưa ra. Một đỉnh nguồn khác cũng được cung cấp. Bây giờ chúng ta phải tìm khoảng cách xa nhất từ nút bắt đầu đến tất cả các đỉnh khác, trong biểu đồ.
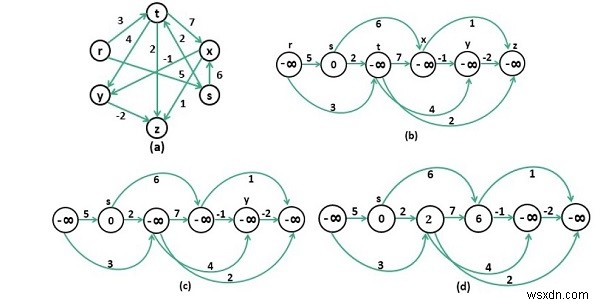
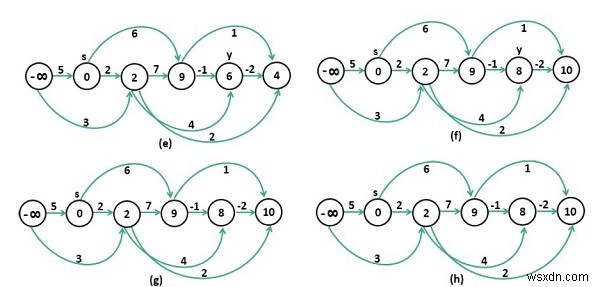
Chúng ta cần sắp xếp các nút trong kỹ thuật sắp xếp tôpô, và kết quả sau khi sắp xếp tôpô được lưu trữ thành một ngăn xếp. Sau đó liên tục xuất hiện từ ngăn xếp và cố gắng tìm khoảng cách xa nhất cho mỗi đỉnh.
Đầu vào và Đầu ra
Input: The cost matrix of the graph. 0 5 3 -∞ -∞ -∞ -∞ 0 2 6 -∞ -∞ -∞ -∞ 0 7 4 2 -∞ -∞ -∞ 0 -1 1 -∞ -∞ -∞ -∞ 0 -2 -∞ -∞ -∞ -∞ -∞ 0 Output: Longest Distance from Source Vertex 1 Infinity 0 2 9 8 10
Thuật toán
topoSort (u, đã truy cập, ngăn xếp)
Đầu vào: nút bắt đầu u, danh sách đã truy cập để theo dõi, ngăn xếp.
Đầu ra - Sắp xếp các nút theo cách cấu trúc liên kết.
Begin mark u as visited for all vertex v, which is connected with u, do if v is not visited, then topoSort(v, visited, stack) done push u into the stack End
LongPath (bắt đầu)
Đầu vào - Nút bắt đầu.
Đầu ra - Danh sách khoảng cách xa nhất của tất cả các đỉnh từ nút bắt đầu.
Begin initially make all nodes as unvisited for each node i, in the graph, do if i is not visited, then topoSort(i, visited, stack) done make distance of all vertices as - ∞ dist[start] := 0 while stack is not empty, do pop stack item and take into nextVert if dist[nextVert] ≠ - ∞, then for each vertices v, which is adjacent with nextVert, do if cost[nextVert, v] ≠ - ∞, then if dist[v] < dist[nectVert] + cost[nextVert, v], then dist[v] := dist[nectVert] + cost[nextVert, v] done done for all vertices i in the graph, do if dist[i] = - ∞, then display Infinity else display dist[i] done End
Ví dụ
#include<iostream>
#include<stack>
#define NODE 6
#define INF -9999
using namespace std;
int cost[NODE][NODE] = {
{0, 5, 3, INF, INF, INF},
{INF, 0, 2, 6, INF, INF},
{INF, INF, 0, 7, 4, 2},
{INF, INF, INF, 0, -1, 1},
{INF, INF, INF, INF, 0, -2},
{INF, INF, INF, INF, INF, 0}
};
void topoSort(int u, bool visited[], stack<int>&stk) {
visited[u] = true; //set as the node v is visited
for(int v = 0; v<NODE; v++) {
if(cost[u][v]) { //for allvertices v adjacent to u
if(!visited[v])
topoSort(v, visited, stk);
}
}
stk.push(u); //push starting vertex into the stack
}
void longestPath(int start) {
stack<int> stk;
int dist[NODE];
bool vis[NODE];
for(int i = 0; i<NODE;i++)
vis[i] = false; // make all nodes as unvisited at first
for(int i = 0; i<NODE; i++) //perform topological sort for vertices
if(!vis[i])
topoSort(i, vis, stk);
for(int i = 0; i<NODE; i++)
dist[i] = INF; //initially all distances are infinity
dist[start] = 0; //distance for start vertex is 0
while(!stk.empty()) { //when stack contains element, process in topological order
int nextVert = stk.top(); stk.pop();
if(dist[nextVert] != INF) {
for(int v = 0; v<NODE; v++) {
if(cost[nextVert][v] && cost[nextVert][v] != INF) {
if(dist[v] < dist[nextVert] + cost[nextVert][v])
dist[v] = dist[nextVert] + cost[nextVert][v];
}
}
}
}
for(int i = 0; i<NODE; i++)
(dist[i] == INF)?cout << "Infinity ":cout << dist[i]<<" ";
}
main() {
int start = 1;
cout << "Longest Distance From Source Vertex "<<start<<endl;
longestPath(start);
} Đầu ra
Longest Distance From Source Vertex 1 Infinity 0 2 9 8 10
