Cây tách rời cạnh tối đa có thể có từ một đồ thị hoàn chỉnh trong C ++

Giả sử chúng ta có một đồ thị hoàn chỉnh; chúng ta phải đếm số cây Spanning Edge Disjoint. Các cây Spanning Edge Disjoint là các cây bao trùm, trong đó không có hai cây nào trong tập hợp có cạnh chung. Giả sử N (số đỉnh) là 4, thì kết quả đầu ra sẽ là 2. Đồ thị hoàn chỉnh sử dụng 4 đỉnh như dưới đây -

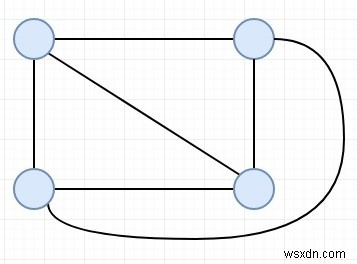
Hai cây khung rời nhau có cạnh giống như -

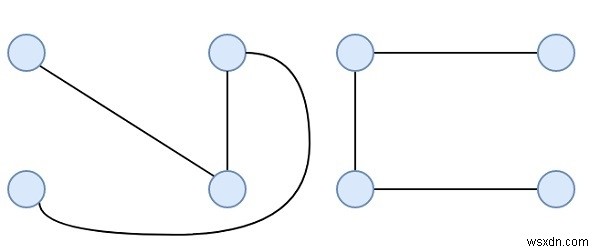
Số lượng tối đa của cây khung rời rạc cạnh từ một đồ thị hoàn chỉnh, với N đỉnh sẽ là $ [\ frac {n} {2}] $

Ví dụ

#include <iostream>
#include <cmath>
using namespace std;
int maxEdgeDisjointSpanningTree(int n){
   return floor(n/2);
}
int main() {
   int n = 4;
   cout << "Maximum Edge Disjoint Spanning Tree: " <<
   maxEdgeDisjointSpanningTree(n);
}

Đầu ra

Maximum Edge Disjoint Spanning Tree: 2